По определению, 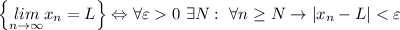
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение 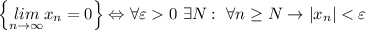
2) 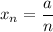
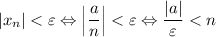
А значит, если взять ![N=\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/0d89e.png) (*),
(*),  . И правда:
. И правда: 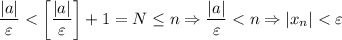
(*) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/ae843.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4) 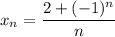

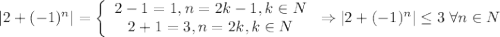
А значит, если взять ![N=\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/a4ca4.png) (**),
(**),  . И правда:
. И правда: ![\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|](/tpl/images/3820/0626/49458.png)
(**) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/698f8.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда 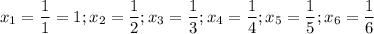
4)

___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x. 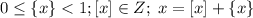

Если поезда встречаются через полчаса, то скорость их сближения равна
75 / 0,5 = 150 км/ч. Обозначим скорость товарного поезда через Х. Тогда скорость пассажирского поезда 150 - Х. Получаем уравнение
75 75 5
- =
Х 150 - Х 12
75 * (150 - Х) - 75 * Х 5
=
Х * (150 - Х) 12
12 * (11250 - 150 * Х) = 5 * Х * (150 - Х)
135000 - 1800 * Х = 750 * Х - 5 * Х²
5 * Х² - 2550 * Х + 135000 = 0
Х² - 510 * Х + 27000 = 0
Х₁ = 60 Х₂ = 450 (не подходит)
Итак, скорость товарного поезда 60 км/ч,
а пассажирского 150 - 60 = 90 км/ч.