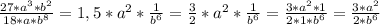
Объяснение:
Степень числа, это произведение множителей, каждый из которых величиной 
, 
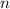раз подряд, где
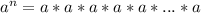
Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого числа вычитают показатель степени делителя:
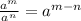
Где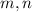 
- любые натуральные числа, с условием, что 
.
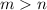Запишем наш пример:
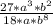
Для наглядности решения данный пример можно разделить на три части, и согласно свойству частного степеней, которое я записал выше можно было проще решить данный пример.
Первой частью будут известные числа:
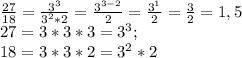(1)
Теперь запишем отдельно деление переменной :
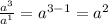(2)
Далее запишем переменную 
:
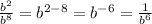(3)
Так как по определению отрицательной степени: 
Теперь совместим (1), (2) и (3):
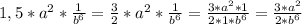- в дальнейшем данную дробь сократить невозможно, это и будет ответ.
Представьте в виде произведения
Применяем формулу:
a^2 - b^2 = (a - b)*(a + b)
Получаем:
(p + q - p + q)* (p + q + p - q) = (p +q)*(2p)