1. -21-a будет отрицательным значением,
2. (-19-a)(a+21) будет отрицательным значением,
3.(a-12)(15-a) будет отрицательным значением,
4.12-a не является отрицательным значением
5. a-15 будет отрицательным значением
6. a+19 не является отрицательным значением
Объяснение:
Число "а" должно быть больше чем -19, но меньше 12 и допустим это число 0. Если мы подставим в первое -21-0 будет число отрицательное и это то что нам нужно. Потом за место а мы везде вставляем 0, допустим то же 2) (-19-0) будет отрицательное значение
Предлагаю заменить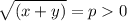
Тогда: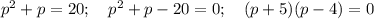
Получаем
p=- 5; p=4.
р>0 => p=4
Перейдем к начальной системе: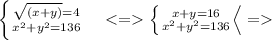
Решим второе уравнение системы:
Отсюда, подставляя получаем:
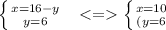
ОТВЕТ: (6;10); (10; 6)