Объяснение:
Функция задана формулой y = 2x - 5. Определите:
1) значение функции, если значение аргумента равно -2;
2) значение аргумента, при котором значение функции равно 13;
3) проходит ли график функции через точку А(-1; -7).
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y = 2x − 5
Таблица:
х -1 0 1
у -7 -5 -3
1)Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х= -2
у=2*(-2)-5= -9 у= -9 при х= -2
2)Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
у=13
13=2х-5
-2х= -5-13
-2х= -18
х=9 у=13 при х=9
3)Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
А(-1; -7)
y = 2x − 5
-7=2*(-1)-5
-7= -2-5
-7= -7, проходит.
2. Постройте график функции y = 2x+ 1. Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно 1;
2) значение аргумента, при котором значение функции равно -3.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y = 2x+ 1
Таблица:
х -1 0 1
у -1 1 3
а)согласно графика при х=1 у=3
б)согласно графика при у= -3 при х= -2
3. Не выполняя построения, найдите координаты точек пересечения графика функции
y = -2x+ 6 с осями координат.
а)График пересекает ось Оу при х=0.
у= -2*0+6=6
Координаты точки пересечения графиком оси Оу (6; 0)
б)График пересекает ось Ох при у=0.
0= -2х+6
2х=6
х=3
Координаты точки пересечения графиком оси Ох (3; 0)
4. При каком значении k график функции y = kx + 4 проходит через точку А(-3; -17)?
Нужно подставить известные значения х и у (координаты точки А) в уравнение и вычислить k:
y = kx + 4
-17=k*(-3)+4
-17= -3k+4
3k=4+17
3k=21
k=7
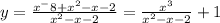
1. Область определения:
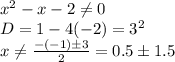
x∈(-∞;-1)∪(-1;2)∪(2;+∞)
2. Найдём точки пересечения с осями:
![y=\frac{x^3+x^2-x-2}{x^2-x-2}=0\\y(0)=-2/-2=1\\x^3+x^2-x-2=0\\ax^3+bx^2+cx+d=0\\a=1;b=1;c=-1;d=-2\\p=\frac{3ac-b^2}{3a^2} =\frac{-3-1}{3} =-4/3\\q=\frac{2b^3-9abc+27a^2d}{27a^3} =\frac{2+9-27*2}{27} =-43/27\\x=\sqrt[3]{\frac{-q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} +\sqrt[3]{\frac{-q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} -\frac{b}{3a} =\\\sqrt[3]{\frac{43}{2*27}+\sqrt{\frac{43^2}{27^2*4}+\frac{-64}{27*27}}} +\sqrt[3]{\frac{43}{2*27}-\sqrt{\frac{43^2}{27^2*4}+\frac{-64}{27*27}}} -\frac{1}{3}=](/tpl/images/3195/0622/32bbc.png)
![=\sqrt[3]{\frac{43}{2*27}+\frac{3\sqrt{3*59}}{27*2} }+\sqrt[3]{\frac{43}{2*27}-\frac{3\sqrt{3*59}}{27*2}}-\frac{1}{3}=\\\frac{\sqrt[3]{2(43+3*\sqrt{3*59})}+\sqrt[3]{2(43-3*\sqrt{3*59})}-2}{6}=1.206...](/tpl/images/3195/0622/a8a2e.png)
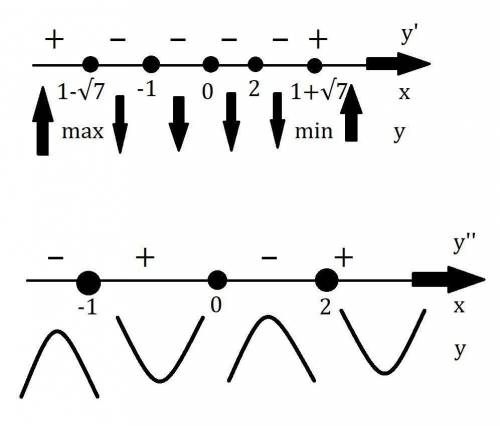
3. Исследование с первой производной:
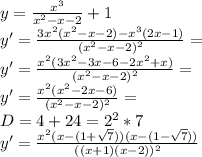
Смотри внизу.
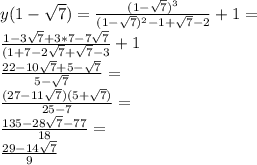
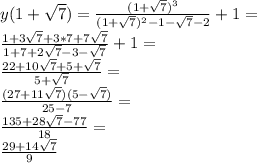
4. Исследование с второй производной:
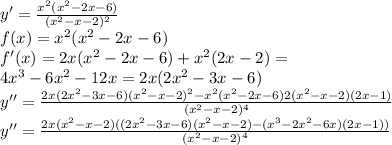
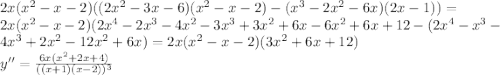
Выражение в скобках в числителе всегда положительное и не равняется нулю, смотри вниз.
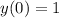
5. Уравнение асимптот:
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:
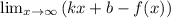
Находим коэффициент k:
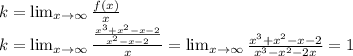
Находим коэффициент b:
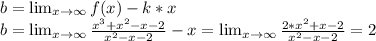
Получаем уравнение наклонной асимптоты: у=x+2
Найдем вертикальные асимптоты. Для этого определим точки разрыва: x_1=-1;x_2=2
Находим переделы в точке x=-1

Это точка разрыва II рода и является вертикальной асимптотой.
Находим переделы в точке x=2

Это точка разрыва II рода и является вертикальной асимптотой.
Опираясь на эти записи можно построить график данной функции.
S=48 км
t=2 ч
v-?
S = v * t отсюда следует, что v = S/t
v = 48 / 2 = 24 км/ч