1) h =13m; 2) t =1+ √1,3+
Объяснение:
h = 18t - 5t²
вначале при полете вверх на камень действует сила тяжести, которая снижает его скорость до полной остановки, а затем он под действием силы тяжести вернется обратно на землю.
1) определим в какой момент времени камень брошенный вверх потеряет скорость (v=0)
v = v0 - gt ; v0-gt = 0
t = v0/g время подъема, t = 10/10 =1 c.
а теперь рассчитаем высоту на которую он поднимется
h = 18v0/g - 5(v0/g)² (для удобства расчета примем g=10)
h = 18*10/10 - 5(10/10)² =18 - 5 =13
h =13 m t = 1 время подъема
2)теперь определим время возврата мяча на землю под действием силы тяжести.
h = v0t + gt²; где v0=0 начальная скорость. g =10
h = gt²
t² = h/g
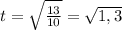 время падения
время падения
полное время полета с момента запуска
t = t1 + t2 = 1 + √1.3
Объяснение:
Дана функция: у = х² - 4х - 5 ;
a) запишите координаты вершины параболы;
Формула: х₀ = -b/2a
x₀ = 4/2 = 2;
y₀ = 2² - 4*2 - 5 = 4 - 8 - 5 = -9.
Координаты вершины параболы (2; -9).
b) запишите ось симметрии параболы;
x = 2;
c) найдите точки пересечения графика с осями координат;
1) при пересечении графиком оси Оу х равен нулю:
у = х² - 4х - 5 ; х = 0
у = 0² -4*0 - 5 = -5;
Координаты пересечения графиком оси Оу (0; -5);
2) при пересечении графиком оси Ох у равен нулю:
у = х² - 4х - 5 ; у = 0
х² - 4х - 5 = 0, квадратное уравнение, ищем корни:
D=b²-4ac =16 + 20 = 36 √D= 6
х₁=(-b-√D)/2a
х₁=(4-6)/2
х₁= -2/2
х₁= -1;
х₂=(-b+√D)/2a
х₂=(4+6)/2
х₂=10/2
х₂=5.
Координаты пересечения параболой оси Ох (-1; 0); (5; 0).
d) постройте график функции.
График - парабола со смещённым центром, ветви направлены вверх.
Таблица
х -3 -2 -1 0 1 2 3 4 5 6 7
у 16 7 0 -5 -8 -9 -8 -5 0 7 16
График прилагается.
e) найдите промежутки убывания и возрастания функции;
Функция возрастает при х∈(2; +∞);
Функция убывает при х∈(-∞; 2).
равно 8
10+8 равно 18 и 18 -8=10