Объяснение:
Для того, чтобы число составленное из цифр 0, 2, 4, 7, 8 было нечетным, то последнее цифра должна быть 7 так как по признаку делимости числа на 2, то число делится на два если его последняя цифра делится на 2, а так как 0, 2, 4, 8 делится на 2, а 7 - не делится, то последняя цифра числа 7.
На оставшиеся места претендуют комбинации из цифр: 0, 2, 4, 8
Нужно выбрать 2 числа из 4 цифр, так как по условие число трехзначное. Число размещений:
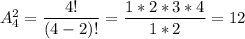
Выбрать 1 элемент из трех возможно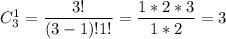 
, так как ноль не может стоять на первом месте. Пусть всего составить различные нечетные трехзначных числа без повторений цифр, тогда 
.
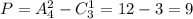sin3acos6a+sin6acos3a=sin(3a+6a)=sin(9a)
sin(9*(3pi/8))=sin(27pi/8)=sin(11pi/8)
sin(11pi/8)=-sqrt[(1-cos11pi/4)/2]
cos(11pi/4)=cos(495)=cos(135)=-(sqrt2)/2
sin(11pi/8)=-sqrt[(1+(sqrt2)/2)/2]
ответ: -sqrt[(1+(sqrt2)/2)/2]