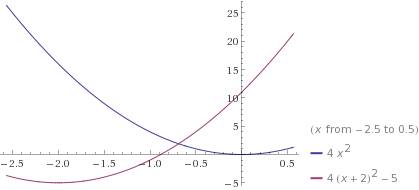
если для первого графика y = 4x^2 вершина находится в точке (0;0), то
ось симметрии параболы - ось OY (уравнение x=0)
то для второго графика ось симметрии сместится влево на 2 (уравнение x = -2, все первое слагаемое обратится в 0 и получится y = -5), т.е. для второго графика вершина опустится вниз по оси OY на 5 единиц и сместится влево на 2 единицы по оси OX
координаты вершины новой параболы (-2;-5), ветви вверх и она в точности повторяет первый график (из новой точки---новой вершины), иными словами
новый график получится параллельным переносом исходного графика вниз по оси OY на 5 единиц и влево по оси OX на 2 единицы
Как я поняла нужно решить 2 квадратных неравенства. Так?
Тогда решаем первое
х2-6х+9<=0
x2-6x+9=0
D=36-4*9=0, то есть корень 1
х=(6+0)/2=3
Значит графиком является парабола, пересекающая ось х в точке3, ветви вверх
Значит квадратный трехчлен нигде не будет <0, но так как нужно еще рассмотреть случай когда он=0, то решением будет точка 3
ответ: 3
2) -х2+12х-36>0 т.е.
(умножаем на -1) х2-12х+36=0
D=144-4*36=0, т.е одно решение
x=12/2=6 Квадратный трехчлен пересекает ось х в точке 6, ветви вниз
Т.е. нет точек когда он>0
ответ: Нет решения или решением является пустое множество
ответ:
P=12/30