как найти точки пересечения графика функции с осями координат?
с осью абсцисс график функции может иметь любое количество общих точек (или ни одной). с осью ординат — не более одной (так как по определению функции каждому значению аргумента ставится в соответствие единственное значение функции).
чтобы найти точки пересечения графика функции y=f(x) с осью абсцисс, надо решить уравнение f(x)=0 (то есть найти нули функции).
чтобы найти точку пересечения графика функции с осью ординат, надо в формулу функции вместо каждого x подставить нуль, то есть найти значение функции при x=0: y=f(0).
примеры.
1) найти точки пересечения графика линейной функции y=kx+b с осями координат.
решение:
в точке пересечения графика функции с осью ox y=0:
kx+b=0, => x= -b/k. таким образом, линейная функция пересекает ось абсцисс в точке (-b/k; 0).
в точке пересечения с осью oy x=0:
y=k∙0+b=b. отсюда, точка пересечения графика линейной функции с осью ординат — (0; b).
например, найдём точки пересечения с осями координат графика линейной функции y=2x-10.2x-10=0; x=5. с ox график пересекается в точке (5; 0).
y=2∙0-10=-10. с oy график пересекается в точке (0; -10).
2) найти точки пересечения графика квадратичной функции y=ax²+bx+c с осями координат.
решение:
в точке пересечения графика с осью абсцисс y=0. значит, чтобы найти точки пересечения графика квадратичной функции (параболы) с осью ox, надо решить квадратное уравнение ax²+bx+c=0.
в зависимости от дискриминанта, парабола пресекает ось абсцисс в одной точке или в двух точках либо не пересекает ox.
в точке пересечения графика с осью oy x=0.
y=a∙0²+b∙0+c=с. следовательно, (0; с) — точка, в которой парабола пересекает ось ординат.
например, найдём точки пересечения с осями координат графика функции y=x²-9x+20.
x²-9x+20=0
x1=4; x2=5. график пересекает ось абсцисс в точках (4; 0) и (5; 0).
y=0²-9∙0+20=20. отсюда, (0; 20) — точка пересечения параболы y=x²-9x+20 с осью ординат.
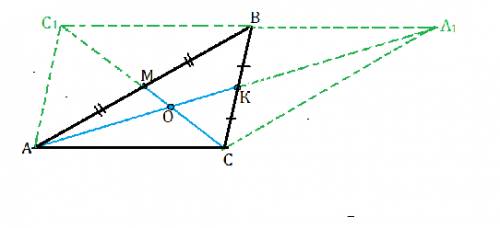
Пусть дан т-к АВС.
Продлим медианы на их длину ( см. рис)
По свойству диагоналей параллелограмма
АА1²+ВС²=2(АВ²+АС²)
и
СС1²+АВ²=2(АС²+ВС²)
Пусть АВ=с, ВС=а
Составим систему уравнений:
[(2*6√7)²+a²=2(c²+14²)
[(2*3√7)²+c²=2(14²+a²)
⇒
[ а²-2с²=2*14² -144*7
[-2а²+с²=2*14²-36*7 домножим на 2 обе стороны этого уравнения.
Сложим уравнения системы:
[а²-2с=2*14² -144*7
[-4а²+2с²=4*14²-72*7
-3а²=6*14²-216*7⇒
а²=112
а=4√7
Подставим найденное значение а в уравнение
а²-2с²=2*14² -144*7 ⇒
112+144*7-2*196=2 с²
с²=364
с=2√91
АВ=2√91
ВС=4√7
---------
Задачу можно решить по т. косинусов.
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины.
Тогда АО=4√7, CO=2√7
Из ∆ АОС
АС²=АО²+СО²-2*АО*СО*cos ∠АОС
cos ∠АОС=(АС²-АО²+СО²):(-2*АО*СО)
cos ∠АОС=[14²-(4√7)²-(2√7)²]:[-2*(4√7)*(2√7]
cos ∠АОС= -56:2*56= -1/2 - это косинус 120º
В ∆ СОК ∠ СОК =180°-120°=60°
ОК=АК:3=2√7
ОК=ОС, угол СОК=60°⇒
∆ СОК - правильный, СК=2√7,
ВС=2 СК=4√7
В Δ АМО ∠ МОА=∠ СОК=60°
АМ²=МО+АО-2*МО*АО*cos∠АОМ
АМ²=(√7)²+(4√7)²-2*(√7)*(4√7)*1/2*cos∠АОМ
АМ²=7+16*7-2*4*7*1/2
АМ²=91
АМ=√91
AB=2√91