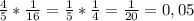
242
Объяснение:
Наименьшее возможное значение суммы трёх неравных членов равно 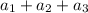 , наибольшее значение суммы двух членов равно
, наибольшее значение суммы двух членов равно 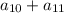 . Значит, если для этих членов неравенство выполняется, то и для любых других гарантированно выполняется.
. Значит, если для этих членов неравенство выполняется, то и для любых других гарантированно выполняется.
Два соседних числа отличаются как минимум на 1, значит, 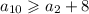 и
и 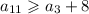 .
.
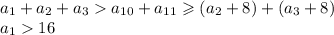
Наименьшее значение первого члена 17, тогда следующий член не меньше 18, третий - не меньше 19 и т.д.
Наименьшая сумма отсюда равна
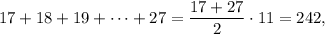
если, конечно, последовательность 17, 18, ..., 27 удовлетворяет условию
Легко проверить, что эта последовательность подходит: действительно, 17 + 18 + 19 = 54 > 53 = 26 + 27
B) 9
Объяснение:
Произведение рационального числа и иррационального числа рационально тогда, и только тогда, когда первое равно 0. (1)
Пусть не так: существует некое рациональное число r, отличное от 0, и иррациональное число n такие, что произведение k=r*n рационально.
Тогда k/r=n рационально. Но n иррационально - противоречие. А значит предположение неверно.
При этом, очевидно, для любого иррационального числа n произведение 0*n=0 - рационально.
a рационально => 3-a=(b√3)/3 рационально
b рационально => b/3 рационально. Но √3 - число иррациональное. Тогда, согласно (1), b/3=0 => b=0 => a+0=3 => a=3
Тогда a²+b²=3²+0²=9