 и
и  . Чтобы найти координату
. Чтобы найти координату  точек пересечения приравняем две функции (они пересекаются, значит приравниваем). Получаем:
точек пересечения приравняем две функции (они пересекаются, значит приравниваем). Получаем:
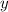 можем найти подставив
можем найти подставив  в выражение первой функции
в выражение первой функции  , а можно сделать проще. Так как пересечение будет с прямой
, а можно сделать проще. Так как пересечение будет с прямой  , то и точки пересечения будут иметь координату
, то и точки пересечения будут иметь координату  . Итак, получилось две точки пересечения с координатами:
. Итак, получилось две точки пересечения с координатами: 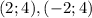 .
.![[0;1]](/tpl/images/0561/5883/90495.png) (этот отрезок по оси
(этот отрезок по оси  ), найдем значения
), найдем значения 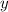 на концах этого отрезка:
на концах этого отрезка: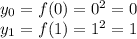
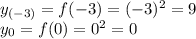

2Sin 2x Cos x = sin2x
2Sin 2xCos x - Sin2x =0
Sin 2x(2Cos x -1) =0
Sin 2x = 0 или 2Cos x -1 =0
2x = πn, где n∈Z 2Cos x =1
x = πn/2 , где n∈Z Cos x = 1/2
x = +- arcCos 1/2 + 2πk. где k∈Z
x = +-π/3 +2πk, где k∈Z
Cумма косинусов
2Cos 6x Cosx + Cos 6x = 0
Cos 6x(2Cos x +1) = 0
Cos 6x = 0 или 2Cos x +1 =0
6x = π/2 +πк, где к∈Z 2Cos x = -1
x= π/12 + πк/6, где к∈Z Cos x = -1/2
х = +- arcCos(-1/2) +2πn, где n∈Z
x = +-π/3 + 2π n, где n∈Z
13) Sin 3x = 2Cos 3x | : Cos 3x≠0
tg 3x = 2
3x = arctg2 + πk, где k∈Z
x = arctg2/3 + πk/3, где k∈Z
14) 2Sin 5x = 3Cos 5x | : Cos 5x ≠0
2tg 5x = 3
tg 5x = 1,5
5x = arctg1,5 + πk, где k∈Z
x = arctg1,5/5 + πk/5, где k ∈Z