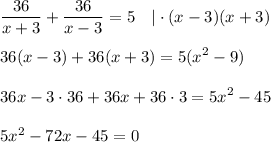
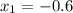 - не удовлетворяет условию
- не удовлетворяет условию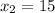 км/ч - скорость лодки в неподвижной воде
км/ч - скорость лодки в неподвижной воде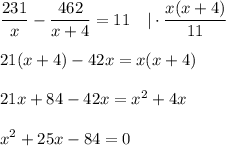
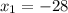 - не удовлетворяет условию
- не удовлетворяет условию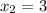 деталей делает ученик в час.
деталей делает ученик в час.2) 4+7=11 (ч) - общее время в пути.
3) 640-35=605 (км)
4) 605:11=55 (км/ч) - скорость машины.
5) 55+5=60 (км/ч) - скорость поезда Предположим, что скорость поезда х км/ч, тогда скорость машины (х-5) км/ч, также из условия задачи известно, что за 4 часа езды на машине и 7 часов езды на поезде туристы проехали 640 км
согласно этим данным составим и решим уравнение:
4(х-5)+7х=640
4х-20+7х=640
11х-20=640
11х=640+20
11х=660
х=660:11
х=60 (км/ч) - скорость поезда.
х-5=60-5=55 (км/ч) - скорость машины Предположим, что скорость машины х км/ч, тогда скорость поезда (х+5) км/ч, также из условия задачи известно, что за 4 часа езды на машине и 7 часов езды на поезде туристы проехали 640 км
согласно этим данным составим и решим уравнение:
4х+7(х+5)=640
4х+7х+35=640
11х+35=640
11х=640-35
11х=605
х=605:11
х=55 (км/ч) - скорость машины.
х+5=55+5=60 (км/ч) - скорость поезда Предположим, что скорость поезда х км/ч, а скорость машины у км/ч, также из условия задачи известно, что за 4 часа езды на машине и 7 часов езды на поезде туристы проехали 640 км, а зная, что скорость поезда больше скорости машины на 5 км/ч
составим и решим систему уравнений:

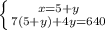
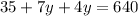

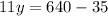
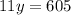
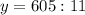
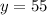 (км/ч) - скорость машины.
(км/ч) - скорость машины.
 (км/ч) - скорость поезда.
(км/ч) - скорость поезда.
ответ: скорость поезда 60 км/ч.
Проверка:
1) 55·4=220 (км) - проехали туристы на машине.
2) 60·7=420 (км) - проехали туристы на поезде.
3) 220+420=640 (км) - весь путь.
2 * 9^X - (2 * A + 3) * 6^X + 3 * A * 4^X = 0
разделив на 9^X, получаем
2 * (4/9)^X - (2 * A + 3) * (2/3)^X + 3 * A = 0
Положив (2/3)^X = T, получаем
2 * Т² - (2 * А + 3) * Т + 3 * А = 0
Дискриминант D = (2 * A + 3)² - 4 * 2 * 3 * A = 4 * A² + 12 * A + 9 - 24 * A =
4 * A² - 12 * A + 9 = (2 * A - 3)²
Тогда корни уравнения T₁₂ = ((2 * A + 3) ± (2 * A - 3)) / 4
или Т₁ = А Т₂ = 3/2
Уравнение имеет 1 корень, если А = 3/2 (корень кратный) или если А ≤ 0 (показательная функция принимает только положительные значения)
Если же А > 0 и A ≠ 3/2, то уравнение имеет 2 корня