1. Решим первое неравенство этой системы:
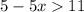
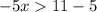
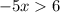
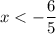
ответ: 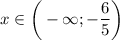
2. Дробь 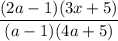 существует, если
существует, если
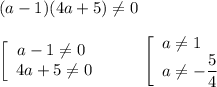
Перед тем как выражать  , нужно рассмотреть случаи, когда дробь
, нужно рассмотреть случаи, когда дробь 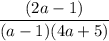 положительная, а когда отрицательная:
положительная, а когда отрицательная:
 знак неравенства меняться не будет (так как делим (умножаем) на положительное число):
знак неравенства меняться не будет (так как делим (умножаем) на положительное число):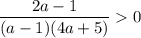
Решим неравенство методом интервалов.
а) ОДЗ: 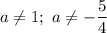
б) Нуль неравенства: 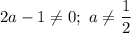
в) Решением данного неравенства будет 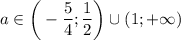 .
.
При таких значениях параметра  знак неравенства меняться не будет:
знак неравенства меняться не будет:
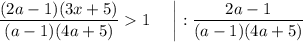
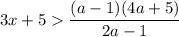
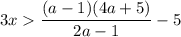
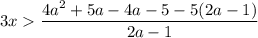
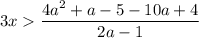
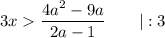
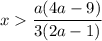
 знак неравенства измениться на противоположный (так как делим (умножаем) на отрицательное число):
знак неравенства измениться на противоположный (так как делим (умножаем) на отрицательное число):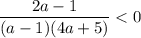
Решим неравенство методом интервалов. Решением данного неравенства будет  .
.
При таких значениях параметра  знак неравенства изменится:
знак неравенства изменится:
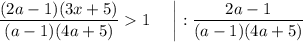
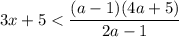
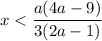
ответ: если  , то
, то 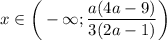 ; если
; если 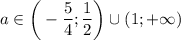 , то
, то 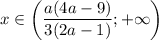 ; если
; если 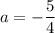 и
и 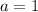 , то неравенство не имеет решений.
, то неравенство не имеет решений.
3. Данная система неравенств решается в зависимости от значений параметра  , поэтому:
, поэтому:
1) Рассмотрим случай, когда решение неравенств пересекается:
Если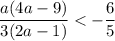 , то есть
, то есть 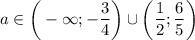 , то в объединении с
, то в объединении с 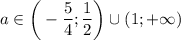 получаем
получаем 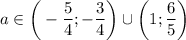
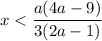 при
при  Если
Если 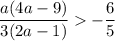 , то есть
, то есть 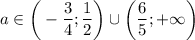 , то в объединении с
, то в объединении с  получаем, что таких
получаем, что таких  не существует, то есть такого варианта эта система не имеет.
не существует, то есть такого варианта эта система не имеет.2) Рассмотрим случай, когда решение неравенств не пересекается (когда система не имеет решений):
Оставшийся промежуток является решением этого варианта:![a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}](/tpl/images/0595/8885/89750.png)
ответ: если  , то
, то 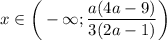 ; если
; если 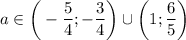 , то
, то 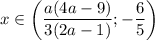 ; если
; если ![a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}](/tpl/images/0595/8885/89750.png) , то система не имеет решений.
, то система не имеет решений.
ay^2+by+c=0
y1×y2=c/a
y1+y2=-b/a
знание данных соотношений позволяем определить знаки корней уравнения. если сумма и произведение положительны, оба корня положительны. если сумма отрицательна, а произведение положительно, оба корня отрицательны. если сумма положительна, а произведение отрицательно - корни имеют разный знак, больший по модулю положителен. Далее подбираются пары чисел, имеющие такое же произведение и проверяются равенством с суммой. папа чисел,дающая верное равенство, является корнями уравнения.
Данная теорема позволяет быстро решать уравнения с целочисленными корнями.