x⁵+8x⁴+24x³+35x²+28x+12=0
Следствие из теоремы Безу гласит: "если многочлен с целыми коэффициентами имеет целый корень, то этот корень является делителем свободного члена".
Тогда корень данного уравнения находится среди делителей числа 12, то есть: ±1; ±2; ±3; ±4; ±6; ±12.
Подставляя значения в уравнения, получим, что x=-2 - корень уравнения.
Составим схему Горнера:
| 1 | 8 | 24 | 35 | 28 | 12 |
————————————
-2 | 1 | 6 | 12 | 11 | 6 | 0 |
Теперь можем разложить на множители исходное уравнение:
(x⁴+6x³+12x²+11x+6)(x+2)=0
Далее действия аналогичные:
Находим корень уравнения x⁴+6x³+12x²+11x+6=0 среди делителей его свободного члена: ±1; ±2; ±3; ±6.
Подставляя значения в уравнение x⁴+6x³+12x²+11x+6=0, получим, что x=-2 - корень уравнения.
Составляем схему Горнера:
| 1 | 6 | 12 | 11 | 6 |
—————————
-2 | 1 | 4 | 4 | 3 | 0 |
Теперь получим такое уравнение:
(x³+4x²+4x+3)(x+2)²=0
Находим корень уравнения x³+4x²+4x+3=0 среди делителей его свободного члена: ±1; ±3.
Подставляя значения в уравнение x³+4x²+4x+3=0, получим, что x=-3 - корень уравнения.
Составляем схему Горнера:
| 1 | 4 | 4 | 3 |
———————
-2 | 1 | 1 | 1 | 0 |
Получим такое уравнение:
(x²+x+1)(x+2)²(x+3)=0
x²+x+1=0 или (x+2)²=0 или x+3=0
∅ x=-2 x=-3
ответ: -3; -2.
1) 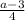
Дробь обращается в ноль, только если числитель равен нулю.
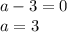
ответ: а=3
2) 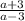
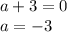
Здесь мы обязательно должны учесть, что знаменатель не должен обращаться в ноль и если получим число а такоеже как для числителя, то должны исключить его из ответа. Это называется областью допустимых значений (ОДЗ).
ОДЗ:
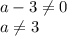
ответ: а=-3
3) 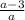
ОДЗ:
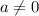
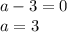
ответ: а=3.
4) 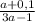
ОДЗ:
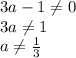
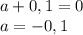
ответ: а=-0,1.
5)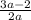
ОДЗ:
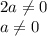
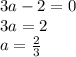
ответ: 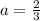
6) 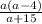
ОДЗ:
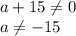
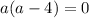
Произведение равно нулю когда хотя бы один из множителей равен нулю.
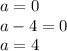
ответ: а=0, а=4.
7) 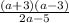
ОДЗ:
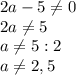
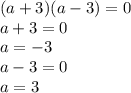
ответ: а=3, а=-3.
8) 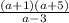
ОДЗ:
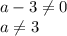
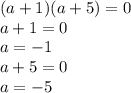
ответ: а=-1, а=-5.
по т пифагора 1/2 другой диагонали равна 39
следовательно диагональ равна 78
перемножив и разделив получим 4056