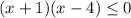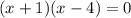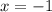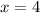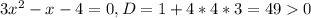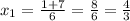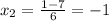Предположим , что степень полинома P(x) не равна степени полинома: x*Q(x).
Тогда степень полинома:
P(x) + x*Q(x) равна либо степени полинома P(x) либо x*Q(x) , в зависимости от того степень какого полинома больше. Но тогда по условию полином большей степени должен иметь 2 степень. Соответственно полином меньшей степени имеет 1 или 0 степень. Но тогда полином : x*P(x)*Q(x) имеет 2 или 3 степень, что невозможно , тк по условию : P(x)*x*Q(x) должен иметь 9+1=10 степень. То мы пришли к противоречию .
Значит степени полиномов P(x) и x*Q(x) должны быть равны.
Тогда тк степень x*P(x)*Q(x) равна 10. То степень полинома P(x) равна:10/2=5
2) Полином :
P(x) +Q(x) имеет степень 3, а полином
P(x)-Q(x) имеет степень 5.
Тогда сумма и разность этих полиномов имеет 5 степень:
То есть 2*P(x) имеет 5 степень и 2*Q(x) имеет 5 степень.
Тогда P(x)*Q(x) имеет 10 степень.