Велосипедист проезжает путь от озера до села со скоростью 8 км/ч, а от села до станции со скоростью - id342372820230516 от Данил20010001 16.05.2023 00:53

Question

Алгебра: Велосипедист проезжает путь от озера до села со скоростью 8 км/ч, а от села до станции со скоростью 10 км/ч, затратив на весь путь 1ч 24 мин. чему равны расстояния от озера до села и от села до станции, если первое меньше второго на 5 км? должна решаться при составления системы

Данил20010001 · Accepted Answer

Пусть х - скорость велосипедиста на пути из А в В. Тогда время, затраченное на путь из А в В = 88/х часов.

Следуя обратно велосипедист 1 час ехал со скоростью х км/ч, таким образом преодолев х километров пути. Затем он сделал остановку на 0,25 часа, и оставшийся путь (88-х км) двигался со скоростью (х+2) км/ч. Таким образом, время затраченное на путь обратно:

1 + 0,25 + (88-х)/(х+2).

По условию, на обратный путь велосипедист потратит столько же времени, сколько и на путь из А в В.

Уравнение:

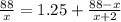
$\frac{88}{x}=1.25+\frac{88-x}{x+2}$

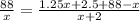
$\frac{88}{x}=\frac{1.25x+2.5+88-x}{x+2}$

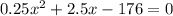
0.25x^2+2.5x-176=0

D = 13.5^2

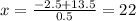$x = \frac{-2.5+13.5}{0.5} = 22$ (км/ч) - скорость велосипедиста

MOGZ ответил