,
, a 
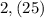
целая часть. У нас она равна 2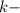
- количество цифр в периоде. У нас их 2
количество цифр до периода. У нас их 0
все цифры, включая период, в виде натурального числа. У нас это 25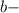
все цифры без периода в виде натурального числа. Их нет.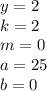
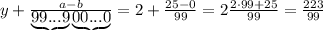
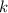подставляется количество 9, а под 
-количество нулей. У нас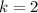 
, значит пишем две цифры 9, а 
, значит, нулей не пишем вообще. Между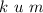 
не стоит знак умножения
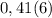
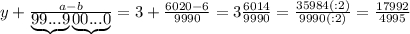
x²+8x+16-(x²-4)=0
x²+8x+16-x²+4=0
8x+20=0
8x=-20
x=-20/8
x=-2,5
(3x+5)(3x-5)-(3x-1)²=10
9x²-25-(9x²-6x+1)=10
9x²-25-9x²+6x-1=10
6x-26=10
6x=36
x=36/6
x=6