Вероятностью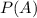 
события 
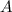при проведении некоторого испытания называют отношение числа тех исходов 
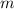, в результате которых наступает событие 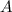, к общему числу 
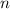всех (равновозможных между собой) исходов этого испытания.
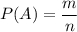
Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти.
Пусть 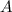- событие, состоящее в том, что из урны, где находится 25 желтых, 15 синих, 10 красных шаров, можно наудачу взять три красных шара.
Из 10 красных шаров нужно выбрать 3 (порядок не имеет значения) - это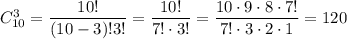 
Выбрать 3 шара из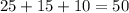 
(порядок не имеет значения) можно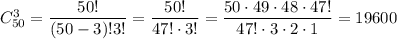 
Следовательно, согласно определению вероятности, вероятность того, что наудачу взятые три шара окажутся красными, будет составлять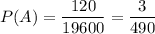 
.
ответ: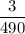 
.
8 y^2 - 7 y - 53 = 2 (4 y^2 - y + 1)
8 y^2 - 7 y - 53 = 8y^2 - 2y + 2
- 7 y - 53 = -2 y + 2
-5y =55
y = -11
Добавлю для некоторых подробное решение, с самого начала, без сокращений, с комментариями
(2y-3)(3y+1)+2(y-5)(y+5)=2(1-2y)^2+6y
Подробное решение
6y^2 + 2y - 9y - 3 + 2(y^2 - 25) = 2(1 - 4y + 4y^2) + 6y
6y^2 + 2y - 9y - 3 + 2y^2 - 50 = 2 - 8y + 8y^2 + 6y
8y^2 - 7y - 53 = 8y^2 - 2y + 2 /сокращаем 8y^2
-7y - 53 = -2y + 2 /Перенесём известные в одну сторону, неизвестные в другую
-7y + 2y = 2 + 53
-5y = 55
y = -11
{x=1+2y { y+2y^2+y-12=0
{x=1+2y 2y^2+2y-12=0.
{x=1+2y y^2+y-6=0;
решим квадратное уравнение y^2+y-6=0
D=1^2-4*1*(-6)=25
y1=(-1+5)/2=2 y2=(-1-5)/2=-3
подставляем в первое уравнение системы x=1+2y
x1=1+2*2=5 x2=1+2*(-3)=-5
ответ: x1=5 y1=2 x2=-5 y2=-3