1. Выпадение 2 очков при 1 бросании = 6, при втором бросании, тоже = 6, значит равновозможных исходов 6*6=36
2. Для того, чтобы 2 очка были наименьшими из выпавших, при первом броске должно выпасть 2, при втором броске - любое количество очков, кроме 1. Или при первом броске - любое, кроме 1, а при втором броске - 2 очка.
3. Возможен вариант выпадения 2 очков и при 1 и при 2 броске, поэтому, при подсчете, вариант это учитывается 2 раза.
3. Выпадение 2 очков из всех, кроме 1 очка = 5, при первом, и 5 при втором броске:
количество благоприятных исходов: 5+5-1=9 ((-1) - выпадение 2 очков в каждом из двух бросаний)
4. Вероятность благоприятного исхода: 9/36=1/4=0.25
ответ: 0.25
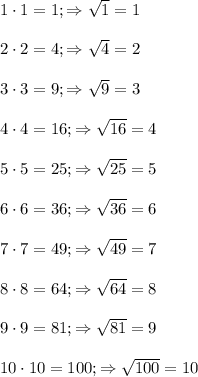
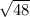 и необходимо найти тот промежуток между целыми числами, которому принадлежит данное число. Смотрим в таблицу квадратов. Находим, что
и необходимо найти тот промежуток между целыми числами, которому принадлежит данное число. Смотрим в таблицу квадратов. Находим, что 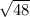 находится между
находится между 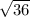 и
и 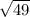 , соответственно,
, соответственно, 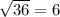 , а
, а 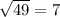 . Таким образом,
. Таким образом, 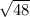 лежит между целыми числами:
лежит между целыми числами: 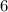 и
и 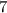
Задача сводится к поиску минимума функции S, описывающей эту площадь. Для этого нужно перейти от функции двух переменных к функции одной переменной.
Размеры цилиндра зависят от двух величин - его высоты и радиуса основания. Выразим высоту цилиндра через известный нам объём и радиус из формулы объёма цилиндра:
Тогда
Для того, чтобы найти минимум функции нужно найти её производную и те точки, в которых она равна нулю.
Осталось подставить в это выражение значение объёма V, вычислить радиус и убедиться в том, что это точка минимума - при прохождении через эту точку производная должна менять знак с минуса на плюс. Тут так и происходит. Найдём высоту цилиндра