Пусть n = x, мне просто так удобнее)
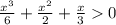
Обе части уравнение умножим на 6:
х³+3х²+2х>0
х(х²+3х+2)>0
х(х+1)(х+2)>0
При любых натуральных значениях х, х(х+1)(х+2) > 0(то есть является натуральным числом)
___________________
2 решение :
Рассмотрим по отдельности каждое слагаемое:
х³/6 > 0 | *6
х³>0
х > 0
То есть х³/6 больше нуля при всех натуральных числах.
____________________________
Если рассмотреть остальные 2 слагаемых, то там будет тоже самое(мне просто лень писать).
____________________________
Если каждое из слагаемых больше нуля, то и сама сумма больше нуля, то есть является натуральным числом)
3*2=6 - произведение двух чисел 3 и 2
2*(3*2)=12 - удвоенное произведение, то есть произведение умножается на 2
Формулы:
(a-b)^2=a^2-2ab+b^2; (a+b)^2=a^2+2ab+b^2;
a) (m-5)^2=m^2-2*m*5+5^2=m^2-10m+25
б) (-m+5)^2=(5-m)^2=5^2-2*5*m+m^2=25-10m+m^2