Question

51 51 выполните действия 1)найдите произведение квадрата одночлена 5xy^2 и куба одночлена (2x^2y^3)^3 2)найдите квадрат произведения одночленов 5nm и 2n^2mk представьте вид одночлена стандартного вида: а) (10a^2y)^3 * (3ay^2)^3= б) (-3x^6y^2)^3 * (-x^2y)^4= решите уровнения а) (3x^2)^2=144 б) (4x)^3=512 в) (2x^2)^2=64 ^-степень *-умножить

Answer 1

Решение смотри на фотографии
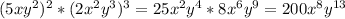
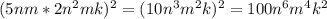
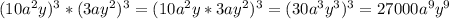
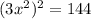
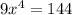
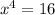
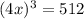
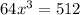
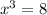
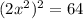
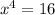
добавляю фотографию

Answer 2

1
$(5xy^2)^2*(2x^2y^3)^3=25x^2y^4*8x^6y^9=200 x^{8} y^{13}$
2
$(5nm*2n^2mk)^2=(10n^3m^2k)^2=100n^6m^4k^2$
3
a)$(10a^2y)^3*(3ay^2)^3=(10a^2y*3ay^2)^3=(30a^3y^3)^3=27000a^9y^9$
b)$(-3x^6y^2)^3*(-x^2y)^4=-27 x^{18}y^6*x^8y^4=-27 x^{26} y ^{10}$
4
а)$(3x^2)^2=144$
$9x^4=144$
$x^4=16$
x=2
x=-2
б)$(4x)^3=512$
$64x^3=512$
$x^3=8$
x=2
в)$(2x^2)^2=64$
$4x^4=64$
$x^4=16$
x=2
x=-2