Question

Решить интеграл. ответ должен получится: 2/3

Answer 1

Как ни странно, ответ здесь действительно 2/3

Объяснение:

Я надеюсь, z здесь никак не связано с комплексными числами. Решаем все это добро на множестве действительных чисел (мне несколько удобнее записывать через x, поэтому буду через х записывать. Думаю, переписать решение, заменив везде x на z, не проблема.)

$\int\limits^\frac{\pi }{2} _0 {\sqrt{cosx(1-cos^2x)} } \, dx =\int\limits^\frac{\pi }{2} _0 {\sqrt{cosx*sin^2x} } \, dx = \int\limits^\frac{\pi }{2} _0 |sinx|{\sqrt{cosx} } \, dx$

Теперь учтем, что пределы интегрирования предполагают, что в этом промежутке синус неотрицателен, а значит, его можно раскрыть со знаком "+".

$\int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \, dx$

Встает вопрос, что делать с этим интегралом. Попробуем интегрировать по частям. Для этого корень будем дифференцировать, а синус интегрировать.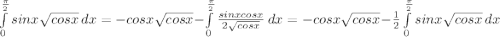 $\int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \, dx = -cosx\sqrt{cosx} - \int\limits^\frac{\pi }{2} _0 {\frac{sinxcosx}{2\sqrt{cosx} } } \, dx=-cosx\sqrt{cosx}-\frac{1}{2} \int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \, dx$

Если не очень понятно про интегрирование по частям, почитай про него. Здесь важно, что: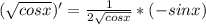 $(\sqrt{cosx})' = \frac{1}{2\sqrt{cosx} }*(-sinx)$, и что 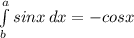$\int\limits^a_b {sinx} \, dx = -cosx$ (без подстановок и прочего) а потом лишь перемножения и вычитание.

Вернемся к интегралу. Занятно получилось, что в выражении спрятано некоторое уравнение относительно как раз нашего интеграла:

$\int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \ dx = -cosx\sqrt{cosx} -\frac{1}{2} \int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \ dx$

Это вообще прекрасно, потому что мы уже фактически нашли наш интеграл:

$\frac{3}{2} \int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \ dx = -cosx\sqrt{cosx}; \int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \ dx = -\frac{2}{3}cosx\sqrt{cosx}$

Естественно, подразумевается, что значение справа вычисляется по двойной подстановке с теми пределами, которые у нас есть.

$-\frac{2}{3}(cos\frac{\pi }{2}\sqrt{cos\frac{\pi }{2} }-cos0\sqrt{cos0})=-\frac{2}{3}(0-1)=\frac{2}{3}$

Вот и получили наш ответ.