Объяснение:
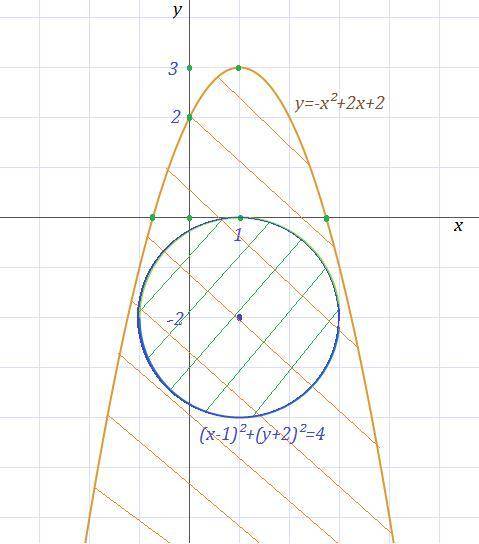
Множество точек, удовлетворяющих неравенству y≤-x²+2x+2 - это часть плоскости ограниченная параболой у= -x²+2x+2 и лежащая внутри этой параболы. Сама парабола у= -x²+2x+2 имеет вершину в точке ( 1,3 ), её ветви направлены вниз .
Множество точек, удовлетворяющих неравенству (x-1)²+(y+2)²≤4 - это часть плоскости, ограниченная окружностью (x-1)²+(y+2)²=4 и находящаяся внутри неё, то есть это круг с центром в точке ( 1, -2) , радиус которого равен R=2 .
Пересечением этих двух множеств являются точки круга вместе с его границей ( окружностью (x-1)²+(y+2)²=4 ) .
На чертеже область заштрихована двумя пересекающимися штриховками.
а). 16а³/5b•35b²/12a⁴= 16a³•35b²/5b•12a⁴=8•7b/6a=4•7b/3a
б). (7m-3)•m³/35m-15= (7m-3)•m³/5(7m-3)=m³/5
в). 6cd/c²-4c•c²-16/18d²=6cd•(c-4)(c+4)/c(c-4)•18d²= 6d(c+4)/18d²= c+4/3d
г). (-5х²/у³)²= 25x⁴/y6
Объяснение:
a). сначала умножаем числитель на числитель и знаменатель на знаменатель; потом упрощаем
б). умножаем разность на числитель (т.к. у этой разности знаменатель 1 и его просто не пишут), в знаменателе можно вынести 5, сокращаем все.
в). в 1 знаменателе можно вынести с, а во втором числители формула
г). степень после скобок относится ко всей дроби, так что возводим в степень 2 и числитель и знаменатель(- при этом уйдет, т.к. степень четная)
2х-5у=-7
Х=3у-5
Теперь вычислим первое(найдем у)
2(3у-5)-5у=-7
6у-10-5у=-7
У=10-7
У=3
Найдем х
Х=3*3-5
Х=4
2)
3х-5у=16
2х+у=2
Из второго выразим у
3х-5у=16
У=2-2х
Решаем первое ищем находим х
3х-5(2-2х)=16
3х-10+10х=16
13х=26
Х=2
находим у
У=2-2*2
У=-2
3)
2х+5у=-7
У=3х-15
2х+5(3х-15)=-7
2х+15х-75=-7
17х=75-7
17х=68
Х=4
У=3*4-15
У=-3
4)
2х-3у=5
Х=6у-2
2(6у-2)-3у=5
12у-4-3у=5
9у=9
У=1
Х=4
5)
5х-4у=12
Х=5у-6
5(5у-6)-4у=12
25у-30-4у=12
21у=42
У=2
Х=10-6
Х=4