первое и второе являются, так как иксы в квадрате))
Сколько существует различных упорядоченных наборов (x,y,z) натуральных чисел x,y,z таких что x+y+z=14?
Таких упорядоченных наборов существует:
(14-1)! / ((3-1)! * (14-3)!) = 13! / (2! * 11!) = 12 * 13 / 2 = 6 * 13 = 78 наборов.
Сколько существует различных упорядоченных наборов (x,y,z) натуральных чисел x,y,z x+y+z=14 x>1,y>2,z>2 или z=2?
Я так понял, что нужно рассмотреть четыре отдельных случая с такими условиями "x>1,y>2,z>2 или z=2". Если нет, и нужно рассмотреть все эти 4 условия вместе, тогда я неправильно понял второй вопрос и нижний ответ вам не подходит.
При x > 1 таких упорядоченных наборов существует:
При y > 2 таких упорядоченных наборов существует:
При z > 2 (как и для y > 2) таких упорядоченных наборов существует:
При z = 2 таких упорядоченных наборов существует:
Объяснение: Ищем ОДЗ. Одновременно должны выполняться три условия :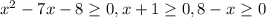 
Решением первого неравенства является объединение полуинтервалов (-∞; -1] ∪ [8; +∞) (вложение), решение второго - [-1; +∞), решение третьего - (-∞; 8]. Условия выполняются одновременно, поэтому нужно искать пересечение этих промежутков - им является множество {-1; 8}.
Так как ОДЗ удовлетворяют только два числа, можем спокойно их подставить в наше неравенство и посмотреть, какие из них являются решением.
При х = -1 получаем: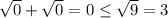 
- верное неравенство. х = -1 - решение.
При х = 8 получаем: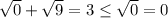 
- неверное неравенство. Следовательно, х = 8 не является решением.
Все случаи перебрали. Запишем ответ.
ОТВЕТ: -1.
" />
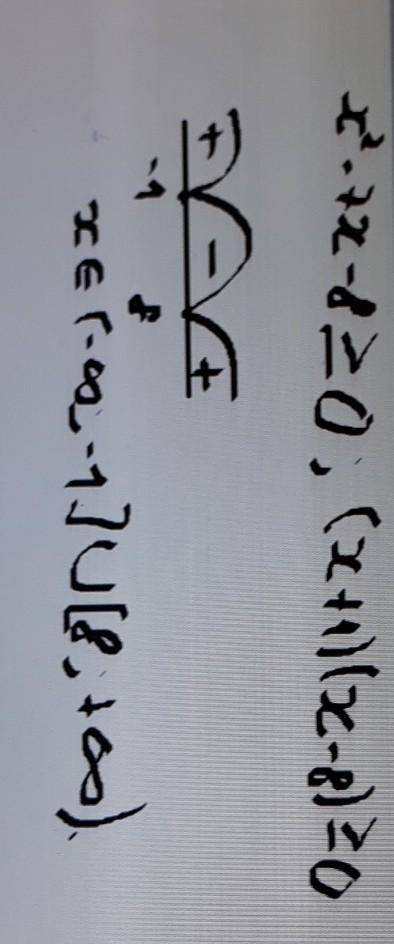Первое и второе да является