Для решения запишем формулу бинома Ньютона:
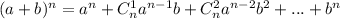
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение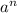 
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение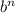 
.
Рассмотрим многочлен 
, где:
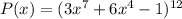
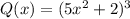
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена :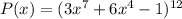
- степень определяется выражением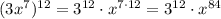 
, то есть степень равна 84
- свободный член равен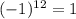 
Для многочлена :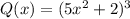
- степень определяется выражением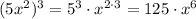 
, то есть степень равна 6
- свободный член равен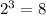 
Наконец, для многочлена 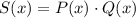получим:
- степень определяется выражением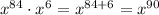 
, то есть степень равна 90
- свободный член равен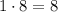 
Сумма степени и свободного члена многочлена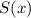 
:
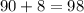
ответ: 98
Рассмотрим два числа A и В
Пусть A=a²+b² B=c²+d² Надо доказать что A*B=x²+z²
A*B=(a²+b²)*(c²+d²)=a²c² + a²d² + b²c² + b²d² = (a²c² + b²d²) + (a²d² + b²c²) + 2*abcd - 2*abcd = *
1. * = (a²c² +2*ac*bd +b²d²) + (a²d² - 2*ad*bc+ b²c²) = (ac + bd)² + (ad - bc)²
2. *= (a²c² - 2*ac*bd +b²d²) + (a²d² + 2*ad*cd+ b²c²) = (ac - bd)² + (ad + bc)²
Таким образом нашли x₁₂ = ac + - bd и z₁₂ = ad - + bc
доказали что если каждое из двух чисел представимо в виде суммы квадратов двух натуральных чисел, то их произведение также можно разложить в сумму квадратов двух целых чисел
cos45° = √2/2
a•b = 2*3*√2/2 = 3√2