Возьмём скорость пропускания второй трубы за х, тогда скорость пропускания первой=х-4
Время, за которое первая труба заполняет 672л воды=672/х-4, а время, за которое 2 труба заполняет 560л воды=560/х. Известно что 2 труба заполняет свой резервуар на 8 минут быстрее, поэтому можно составить уравнение:
672/(х-4) - 560/х=8 домножаем всё на х(х-4) сразу укажем что х не может быть равен 4 (тк при этом идёт деление на ноль чего делать нельзя)
получаем:
672х-560(х-4)=8х(х-4)
672х-560х+2240=8х^2-32х переносим всё в правую часть и считаем
8х^2-144х-2240=0 разделим всё на 8
х^2-18х-280=0
D=18*18+4*280=324+1120=38^2
отсюда х1=(18-38)/2=-10(пост корень тк скор пропускания не может быть отриц)
х2=18+38/2=28
Значит 1 труба пропускает 28-4=24л воды а вторая-28л воды
1)Решение системы неравенств [-2, (-1+√73)/4]
2)Решение системы неравенств х∈(0,2, 1)
Объяснение:
1. Решите систему неравенств:
3х+4≤4х+6
х-5≤4-2х²
Во втором неравенстве перенесём все члены уравнения в левую часть, приравняем к нулю и решим, как квадратное уравнение:
х-5-4+2х²≤0
2х²+х-9=0
х₁,₂=(-1±√1+72)/4
х₁,₂=(-1±√73)/4
х₁=(-1-√73)/4 ≈ -9,5
х₂=(-1+√73)/4 ≈ 7,5
Начертим СХЕМУ параболы, которую обозначает данное уравнение (ничего вычислять не надо). Просто начертим схематично оси, параболу с ветвями вверх, и отметим на оси Ох точки х₁ ≈ -9,5 и
х₂ ≈ 7,5. Ясно видно, что у<0 при х от -9,5 до 7,5, то есть,
решение второго неравенства х∈[(-1-√73)/4, (-1+√73)/4]
Решим первое неравенство.
3х+4≤4х+6
3х-4х ≤6-4
-х ≤2
х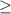
-2 знак меняется
Решение первого неравенства х∈[-2, ∞).
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Решение системы неравенств [-2, (-1+√73)/4] х от -2 до 7,5.
Неравенства нестрогие, скобки квадратные.
2. Решите двойное неравенство -3<2-5х<1
Решается как система:
2-5х>-3
2-5х<1
-5х> -3-2
-5x<1-2
-5x> -5
-5x< -1
x<1 знак меняется x ∈(-∞, 1) решение 1-го неравенства
x>0,2 знак меняется x ∈(0,2, ∞) решение 2-го неравенства
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Решение системы неравенств х∈(0,2, 1)
Неравенства строгие, скобки круглые.
6x(16x⁴-1)=0
6x=0
16x⁴-1=0
x=0
16x⁴=1
x=0