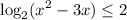
D(f): x^2 - 3x > 0 ⇒ x ∈ (-∞, 0) U (3, +∞)
![x^2-3x\leq4\\x^2-3x-4\leq0\\(x-4)(x+1)\leq0\\x \in [-1, 4]\\](/tpl/images/0352/9623/11c8c.png)
с учетом D(f): ![x \in [-1, 0) \cup (3, 4]](/tpl/images/0352/9623/e9285.png)
рассмотрим четырехугольник авсе
1. отрезок вд равен отрезку ед (по условию),
2. отрезок сд равен отрезку ад (вд - медиана),
следовательно, четырехугольник авсе - параллелограмм ( по свойству диагоналей параллелограмма).
значит, прямые вс и ае параллельны.
рассмотрим углы всд и еад: прямая вс параллельна ае ( по свойству параллелограмма), ас - секущая (пересекает обе прямые), значит угол всд = еад = 40 градусов.
угол вае равен сумме углов вад и еад, значит угол вае = 40 + 56 = 96 градусов.
ответ: угол вае равен 96 градусов.
При решении этих неравенств надо понимать, что графиком квадратичной функции является парабола. Ветвями вверх или вниз. Если хорошо понимать, как проходит парабола,легко поставить знаки квадратичной функции и потом ответить на вопрос задания.
а) х² - 6х +8 > 0
Корни 2 и 4
-∞ (2) (4) +∞
+ - + знаки квадратичной функции
решение неравенства
ответ: х∈(-∞;2)∪(5;+∞)
б) х² + 6х +8 < 0
корни -2 и -4
-∞ (-4) (-2) +∞
+ - + знаки квадратичной функции
решение неравенства
ответ: х∈(-4; -2)
в) -х² -2х +15 ≤ 0
корни -5 и 3
-∞ [-5] [3] +∞
- + - знаки квадратичной функции
решение неравенства
ответ: х∈ (-∞; -5]∪ [3; + ∞)
г) -5х² -11х -6 ≥ 0
корни -1 и -1,2
-∞ [-1,2] [-1] +∞
- + - знаки квадратичной функции
решение неравенства
ответ: х ∈ [-1,2; -1]
д) 9x² -12x +4 > 0
D = 0 корень один
х = 2/3
-∞ (-2/3) +∞
+ + знаки квадратичной функции
решение неравенства
ответ: х∈ (-∞; 2/3)∪ (2/3; +∞)
е) 4х² -12х +9 ≤ 0
D = 0, корень один х = 3/2
-∞ [3/2] +∞
+ + знаки квадратичной функции
∅
ОДЗ: x²-3x>0
x∈(-∞;0)∪(3;+∞)
log2(x²-3x)≤2
log2(x²-3x)≤log2(4)
x²-3x≤4
x²-4x+x-4≤0
x(x-4)+(x-4)≤0
(x-4)(x+1)≤0
x∈[-1;4]
ответ: x∈[-1;0)∪(3;4]