у(наиб) = 32 ( в точке х=2)
у(наим) = 5 ( в точке х=1)
На границах интервала.
Объяснение:
Для того, чтобы найти наибольшее и наименьшее значение функции нам необходимо:
Найти все стационарные точки.Найти все критические точки. Проверить границы интервала. Пункт 1 - стационарные точки:Данные точки ищутся с производной. Найдем производную данной функции:
x'(t) = 8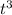
- 3.
Приравниваем производную к 0:
8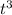 - 3 = 0
t = ±![\sqrt[3]{\frac{3}{8} }](/tpl/images/1201/0058/69c06.png)
= ±![\frac{\sqrt[3]{3} }{2}](/tpl/images/1201/0058/4c079.png)
- однако, эти точки не входят в наш интервал.
Таковых у нас нет, т.к. критические точки - это стационарные точки, но которые не входят в ОДЗ. (У нас ОДЗ от (-∞;∞+)).
Пункт 3 - границы графика:Подставляем значения границ интервала и находим значения в этих точках:
x(1)=2*1^4−3*1+6 = 5
x(2)=2*2^4−3*2+6 = 32
Следовательно, это и есть наибольшее и наименьшее значение функции на заданном интервале.
1)18 (машин на второй стоянке)
36 (машин на первой стоянке)
29 (машин на третьей стоянке)
2)10 (бочек на втором стеллаже)
27 (бочек на третьем стеллаже)
81 (бочка на первом стеллаже)
Объяснение:
1. На трёх стоянках 83 автомобиля, на первой в два раза больше, чем на второй, а на третьей на 7 машин меньше , чем на первой. Сколько машин на каждой стоянке?
1)х - машин на второй стоянке
2х - машин на первой стоянке
2х-7 - машин на третьей стоянке.
По условию задачи всего 83 машины, уравнение:
х+2х+2х-7=83
5х=83+7
5х=90
х=90/5
х=18 (машин на второй стоянке)
18*2=36 (машин на первой стоянке)
36-7=29 (машин на третьей стоянке)
Проверка:
18+36+29=83 (маш.)
2) На трёх стеллажах 118 бочек, причём на третьем в три раза меньше , чем на первом и на 17 больше чем втором. Сколько бочек на каждом стеллаже?
х - бочек на втором стеллаже
х+17 - бочек на третьем стеллаже
3(х+17) - бочек на первом стеллаже
По условию задачи всего 118 бочек, уравнение:
х+х+17+3(х+17)=118
2х+17+3х+51=118
5х=118-68
5х=50
х=10 (бочек на втором стеллаже)
10+17=27 (бочек на третьем стеллаже)
27*3=81 (бочек на первом стеллаже)
Проверка:
10+27+81=118.
х^6-x^2*y^4=x²(x^4-y^4)=x²(x²-y²)(x²+y²)=x²(x-y)(x+y)(x²+y²)