846875
Объяснение:
Всего 6-значных чисел 900000: на первое место можно поставить одну из 9 цифр, на оставшиеся - любую из 10.
Посчитаем, у скольких чисел произведение цифр не делится на 4. Такое бывает в двух случаях:
Произведение цифр нечётное, тогда все цифры нечётные, на каждое место можно независимо выбирать один из 5 вариантов цифры. Таких чисел
Произведение цифр делится на 2, но не на 4, тогда в числе одна из цифр 2 или 6, а остальные - нечетные. Выбрать место для четной цифры можно а после этого расставить цифры - 
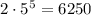Всего получаем 
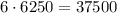чисел.Общее количество чисел, произведение цифр которых не делится на 4, равно 
, значит, искомое количество равно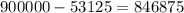 
x1 = -re(acos(-3)) + 2*pi - i*im(acos(-3))
x2 = 2*pi - i*im(acos(4))
x3 = re(acos(-3)) + i*im(acos(-3))
x4 = re(acos(4)) + i*im(acos(4))
Объяснение:
x1 = -re(acos(-3)) + 2*pi - i*im(acos(-3))
x2 = 2*pi - i*im(acos(4))
x3 = re(acos(-3)) + i*im(acos(-3))
x4 = re(acos(4)) + i*im(acos(4))
x1 = 3.14159265358979 + 1.76274717403909*i
x2 = 6.28318530717959 - 2.06343706889556*i
x3 = 3.14159265358979 - 1.76274717403909*i
x4 = 2.06343706889556*i
сумма
-re(acos(-3)) + 2*pi - i*im(acos(-3)) + 2*pi - i*im(acos(4)) + i*im(acos(-3)) + re(acos(-3)) + i*im(acos(4)) + re(acos(4))
=
4*pi + re(acos(4))
произведение
(((-re(acos(-3)) + 2*pi - i*im(acos(-3)))*(2*pi - i*im(acos(4*(i*im(acos(-3)) + re(acos(-3*(i*im(acos(4)) + re(acos(4)))
=
-(2*pi - i*im(acos(4)))*(i*im(acos(-3)) + re(acos(-3)))*(i*im(acos(4)) + re(acos(4)))*(-2*pi + i*im(acos(-3)) + re(acos(-3)))
(3х-2)²=9х²-12х+4
(3х-2)²-применяем формулу сокращенного умножения