
Вероятность определяется как отношение числа благоприятных исходов к общему числу исходов.
Всего имеется 2·29=58 вопросов по теории. Общее число возможностей выбрать 2 из них для включения в билет 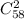 . Однако, чтобы оба вопроса были выученными выбирать надо из их количества. Число выбрать 2 вопроса из выученных
. Однако, чтобы оба вопроса были выученными выбирать надо из их количества. Число выбрать 2 вопроса из выученных 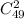 .
.
Таким образом, вероятность ответа на теорию: 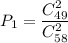
Всего задач 29, но подготовленных только 25. Значит, вероятность решения задачи: 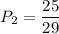
События ответа на теорию и решения задачи независимы, значит полученные вероятности перемножаются:

ответ: 9800/15979
Вероятность того, что из второго ящика переложили в первый ящик стандартную деталь равна  , то в первом ящике будет 51 деталей из них 19 стандартных. Вероятность того, что извлеченная деталь из первого ящика окажется стандартной равна
, то в первом ящике будет 51 деталей из них 19 стандартных. Вероятность того, что извлеченная деталь из первого ящика окажется стандартной равна 
Аналогично, из второго ящика не стандартную деталь переложить в первый ящик можно с вероятностью 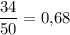 . Тогда в первом ящике будет 51 деталей из них 18 стандартных. Вероятность того, что из первого ящика выбранная деталь - стандартная, равна
. Тогда в первом ящике будет 51 деталей из них 18 стандартных. Вероятность того, что из первого ящика выбранная деталь - стандартная, равна 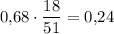
Искомая вероятность: 
Вторая задача. Число всевозможных исходов равно числу выбрать 4 человек из 6+5=11, т.е.  из них ищем благоприятные исходы: выбрать 2 мальчика и 2 девочки:
из них ищем благоприятные исходы: выбрать 2 мальчика и 2 девочки: 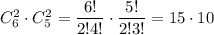
Искомая вероятность: 