a_1,\ a_1+d,\ a_1+2d,\ \ldots,\ a_1+(n-1)d, \ \ldots Так что ~n-й член арифметической прогрессии равен ~{a_n}={a_1}+{ \left( n-1 \right) }d Более точно: последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из предыдущего добавлением к нему постоянного числа d (шага или разности прогрессии). Иначе говоря, для всех элементов прогрессии, начиная со второго, выполнено равенство: a_n=a_{n-1} + d \quad Любой член прогрессии может быть вычислен по формуле: a_n=a_1 + (n-1)d \quad \forall n \ge 1 (формула общего члена) Шаг прогрессии может быть вычислен по формуле: d=\frac{a_n-a_m}{n-m}, если n\neq m Если шаг d > 0, прогрессия является возрастающей; если d < 0, — убывающей.
9x^2+9y^2=13 9x^2+9y^2=13 9(4/9y^2)+9y^2=13 4/y^2+9y^2=13
3xy=2 x=2/3y x=2/3y x=2/3y
4+9y^4=13y^2 y^2 назначим на z 9z^2-13z+4=0
x=2/3y D=25
z1=13+5/18=1
z2=13-5/18=4/9
(y1)^2=1 (y2)^2=4/9 x1=2/3(y1) x2=2/3(y2)
y1=1 y3=2/3 x1=2/3 x3=1
y2=-1 y4=-2/3 x2=-2/3 x4=-1
ответ:{(2/3;1);(-2/3;-1);(1;2/3);(-1;-2/3)}
1) cos2x=-2
нет решений
-1<=cos2x<=1
2) sin4x=0
arcsin0=0
4x = пи*n
x=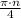
n пренадлежит Z
3) sinx/2=-1/2
arcsin -1/2 = - пи/6
n пренадлежит Z
4) )cos2x=1/2
arccos 1/2 = пи/3
2x= +- пи/3 + 2*пи*n
x= +- пи/6 + пи*n
n пренадлежит Z
5) tg^2x=tgx
tgx=0
arctg0=0
x=пи*n
n пренадлежит Z