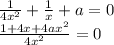
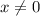и перейдем к следующему уравнению: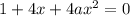
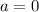, то получим линейное уравнение: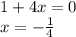
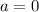удовлетворяет заданному условию.
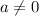, то получаем квадратное уравнение, наличие решений у которого зависит от дискриминанта: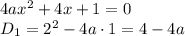
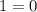, значит остается единственный вариант: приравнять дискриминант к нулю и проверить, будет ли уравнение в этом случае иметь единственный корень: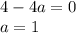
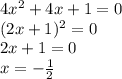
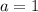также удовлетворяет заданному условию.
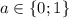, тогда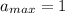 
y'=-4sinx+15
sinx=15/4 т.е. уравнение не имеет решения
y(0)=4+5=9 минимум
y(3п/2)=5+15п/2+4cоs(3п/2)=5+15п/2