Данная система уравнений не имеет решений.
Объяснение:
Имеет ли решение система уравнений и сколько?
4х+3у=4
6у+8х=1 методом сложения
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе нужно первое уравнение умножить на -2:
-8х-6у= -8
6у+8х=1
Складываем уравнения:
-8х+8х-6у+6у= -8+1
0= -7
Данная система уравнений не имеет решений.
1) а = - 3; 2) а = 9; 3) a = -0.6; 4) а = ±1; ±2; ±4; ±5; ±10; ±20;
Объяснение:
1)
Уравнение
(a + 3) · x = -5
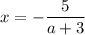
При а = - 3 выражение не имеет смысла. соответственно и уравнение корней не имеет
2)
Уравнение
(a - 9) · (x + 5) = 0
а = 9
0 · (x + 5) = 0 при любых х
Если а = 9, то решением уравнения является любое число
3)
Уравнение
a · (x + 5) = -3
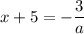
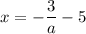
x = 0
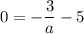
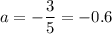
При а = - 0,6 х = 0
4)
Уравнение
ах = -20
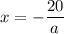
Делители числа 20
20 = 1 · 2 · 2 · 5
Следовательно, х ∈ Z при а = 1; 2; 4; 5; 10; 20;
a также х ∈ Z при а = -1; -2; -4; -5; -10; -20;