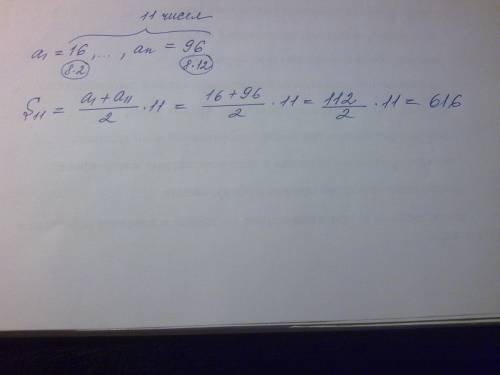
16, 24,32,40,48,56,64, 72,80,88,96
S11=(16+96)*11/2=616
1)Решение системы уравнений х=1
у=2
3)Решение системы уравнений х=1
у=1
5)Решение системы уравнений х=1
у=2
7)Решение системы уравнений х= -1
у=1
Объяснение:
1)2х+у=4
3х-2у= -1
Выразим у через х в первом уравнении, подставим выражение во второе уравнение и вычислим х:
у=4-2х
3х-2(4-2х)= -1
3х-8+4х= -1
7х= -1+8
7х=7
х=1
у=4-2х
у=4-2*1
у=2
Решение системы уравнений х=1
у=2
3)3х+у=4
5х+3у=8
Выразим у через х в первом уравнении, подставим выражение во второе уравнение и вычислим х:
у=4-3х
5х+3(4-3х)=8
5х+12-9х=8
-4х=8-12
-4х= -4
х=1
у=4-3х
у=4-3*1
у=1
Решение системы уравнений х=1
у=1
5)3х-у=1
2х+3у=8
Выразим у через х в первом уравнении, подставим выражение во второе уравнение и вычислим х:
-у=1-3х
у=3х-1
2х+3(3х-1)=8
2х+9х-3=8
11х=8+3
11х=11
х=1
у=3х-1
у=3*1-1
у=2
Решение системы уравнений х=1
у=2
7)3х+2у= -1
2х-у= -3
Выразим у через х во втором уравнении, подставим выражение в первое уравнение и вычислим х:
-у= -3-2х
у=3+2х
3х+2(3+2х)= -1
3х+6+4х= -1
7х= -1-6
7х= -7
х= -1
у=3+2х
у=3+2*(-1)
у=3-2
у=1
Решение системы уравнений х= -1
у=1
х∈(-∞; -9) ∪ (9; + ∞)
Объяснение:
Перший іб:
x² > 81
1) Спочатку знайдемо корені рівняння:
х² = 81
x = ± √81 = ± 9
2) Тепер розглянемо, у яких випадках х² > 81:
Якщо х < -9, то х² > 81
Якщо х = -9, то х² = 81
Якщо -9 < х < 9, то х² < 81
Якщо х = 9, то х² = 81
Якщо х > 9, то х² > 81
Таким чином, ми з’ясували що х² > 81 при х∈(-∞; -9) ∪ (9; + ∞)
Однак, це рівняння можна було розв’язувати і іншим , більш зручним - використовуючи модуль:
х² > 81 <=> |х| > 81
Далі залишається лише розв’язати це рівняння з модулем. Розв’язок у прикріпленому файлі —>