переходи по ссылке там ответ
Ну или не переходи
Решите систему неравенств:
x²-3x+9>0
x²≤36
Решить первое неравенство:
x² - 3x + 9 > 0
Приравнять к нулю и решить квадратное уравнение:
x² - 3x + 9 = 0
D=b²-4ac =9 - 36 = -27
D < 0
Уравнение не имеет действительных корней.
Значит, неравенство выполняется всегда или не выполняется никогда.
Подставить в неравенство произвольное значение х:
х = 0;
0 - 0 + 6 > 0, выполняется.
Значит, неравенство верно при любом значении х.
Решение первого неравенства: х∈(-∞; +∞).
Решить второе неравенство:
x² ≤ 36
Приравнять к нулю и решить квадратное уравнение:
x² = 36 неполное квадратное уравнение
х = ±√36
х₁ = -6;
х₂ = 6.
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= -6 и х= 6.
Решение второго неравенства: х∈[-6; 6].
Неравенство нестрогое, скобки квадратные.
Отметить на числовой оси интервалы решений двух неравенств и найти пересечение решений, это будет решение системы неравенств.
Пересечение решений: х∈[-6; 6].
Случайная величина X распределена по биномиальному закону.
Всего n = 7 испытаний. Вероятность успеха в одном испытании равна p = 0.4, тогда q = 1 - р = 0.6
1) Вероятность того, что стрелок попадет в цель ни разу
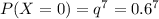
2) Вероятность того, что стрелок попадет в цель один раз
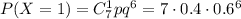
3) Вероятность того, что стрелок попадет в цель два раза
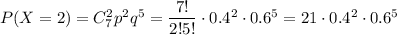
4) Вероятность того, что стрелок попадет в цель три раза
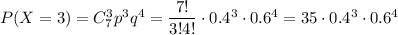
5) Вероятность того, что стрелок попадет в цель четыре раза
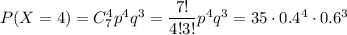
6) Вероятность того, что стрелок попадет в цель пять раз
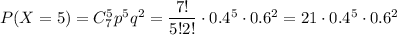
7) Вероятность того, что стрелок попадет в цель шесть раз
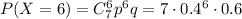
8) Вероятность того, что стрелок попадет в цель 7 раз
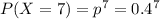
Закон распределения случайной величины X:
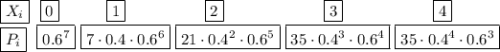
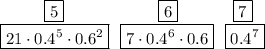
(5p²-8q)²=25p⁴-80p²q+64q²