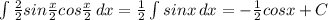
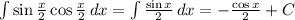
ответ: 36 бусин.
Объяснение:
Так как всего бусин - 56 шт., а красных, зелёных и голубых - всего 11+18+19=48 шт., то чёрных и белых бусин вместе - всего 56-48=8 шт. Поэтому невозможно взять ни 10 чёрных, ни 10 белых бусин. В самом худшем случае сначала будут взяты все чёрные и белые бусины, затем - 9 красных, затем - 9 зелёных и потом - 9 голубых: тогда следующая бусина будет либо 10-й красной, либо 10-й зелёной, либо 10-й голубой. Таким образом, для гарантированного взятия 10 бусин одного цвета нужно взять 8+9+9+9+1=36 бусин.