V(л) = 16,5 км/час - скорость лодки
V(р) - скорость реки
V(л) + V(р) - скорость лодки по течению реки
V(л) - V(р) - скорость лодки против течения реки
S - путь в один конец
Тогда время будет:
по течению:
t(1) = S / (V(л) + V(р)) = 2ч 20мин . = 2 1/3 часа = 7/3 часа
Отсюда
S = 7/3 * (V(л) + V(р))
по течению:
t(2) = S / (V(л) - V(р))= 2ч 20мин - 28 мин = 7/3 часа - 28/60 часа=7/3 - 7/15 часа = 35/15 - 7/15 = 28/15 часа
Отсюда
S = 28/15 * (V(л) - V(р))
приравнять S в обоих случаях и решить уравнения
(см. объяснение)
Объяснение:
79:
Выразим 
из второй строки системы:
Подставим его в первую строку системы:
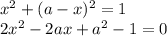
Берем дискриминант, деленный на четыре, и приравниваем его к нулю:
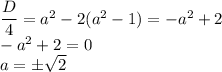
Итого при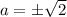 
исходная система уравнений имеет ровно одно решение.
80:
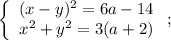
В первой строке системы имеем график двух параллельных прямых, равноудаленных от прямо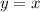й 
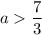при 
. При 
графиком будет прямая
Во второй строке системы имеем уравнение окружности с радиусом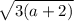 
и центром в точке 
.
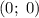Тогда, при 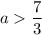каждая прямая пересекает окружность столько же раз, сколько другая.
Очевидно, что сразу возьмем в ответ .
Покажем, что случая, когда обе прямые касаются окружности, не существует.
По формуле расстояния от точки до прямой этот случай можно описать так:
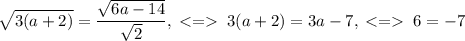, неверно.
Итого при исходная система уравнений имеет ровно два различных решения.
81:
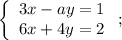
Значение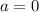 
не подходит.
При 
:
Бусконечное число решений будет, если коэффициенты угла наклона и смещения прямых совпадают.
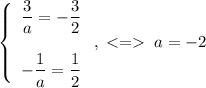
Итого при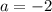 
исходная система имеет бесконечное число решений.
Задание выполнено!
1
Объяснение:
(х-у)(х+у)/(3х^2) •х/(3(х-у))=(х+у)/(9х)=(√3 +√(3•64))/(9√3)=√3(1+√64) (9√3)=(1+8)/9=9/9=1