![y=3x^2;\\ x\in[-1;2];\\ y_{max}-?;\\ y'=3\cdot2\cdot x^{2-1}=6x;\\ x=0\ \ \ local \ \ \ minimum\\ y(-1)=3\cdot(-1)^2=3;\\ y(2)=3\cdot2^2=3\cdot4-12;\\ y_{max}=12](/tpl/images/0364/8566/68808.png)
__-___
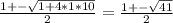
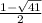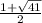_______+___x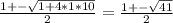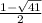__-___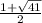_________+___x
пусть а, a+d, a+2d - три числа, образующие арифмитическую прогрессию, тогда
a+8, a+d, a+2d - три числа образующие геометричесскую прогрессию
отсюда и из условия имеем
a+8+a+d+a+2d=26 (условие задачи - сумма членов геометричесской прогрессии равна 26)
3a+3d=18
a+d=6 (*)
d=6-a
(a+d)^2=(a+8)(a+2d) (использовано свойство, если дано три последовательные члены геометрической прогрессии, то квадрат среднего равен произведению первого и третьего члена)
6^2=(a+8)(12-a) (используем (*) )
36=12a+96-a^2-8a
a^2-4a-60=0
D=256=16^2
a1=(4+16)/2=10
a2=(4-16)=-6
b[1]=a=10
b[2=]a+d=6
q=b[2]/b[1]=6/10=0.6
или
b[1]=a=-6
b[2]=a+d=6
q=b[2]/b[1]=6/(-6)=-1
