такое число будет 16061 тогда
15951-16061=110
110/2=55км/ч
Відповідь:
S6 = -2405/9; S6 = 1820/9
Пояснення:
Sn = b1 *(q^n - 1)/(q - 1)
S3 = b1 * (q^3 - 1)/(q - 1)
195 = 135 * (q^3 - 1)/(q - 1)
(q^3 - 1)/(q - 1) = 195/135 = 39/27
(q - 1) * (q^2 + q + 1)/(q - 1) = 13/9
q^2 + q + 1 - 13/9 = 0
q^2 + q - 4/9 = 0
Розв'язуємо квадратне рівняння
D = 1 - 4 * (-4/9) = 25/9
q1 = (-1 - 5/3)/2 = -4/3
q2 = (-1 + 5/3)/2 = 1/3
S6 = 135 * (q^6 - 1)/(q - 1) = 135 * (q^3 - 1)*(q^3 + 1)/(q - 1) = 135 * (q - 1) * (q^2 + q + 1)*(q^3 + 1)/(q - 1) = 135 * (q^2 + q + 1)*(q^3 + 1)
1) S6 = 135 * ((-4/3)^2 - 4/3 + 1)*((-4/3)^3 + 1)
S6 = 135 * (16/9 - 4/3 + 1) * (-64/27 + 1)= 135 * (13/9)*(-37/27) = 5 * 13/9 * (-37) = -2405/9
2) S6 = 135 * ((1/3)^2 + 1/3 + 1)*((1/3)^3 + 1) = 135 * 13/9 * 28/27 = 5 * 13 * 28/9 = 1820/9
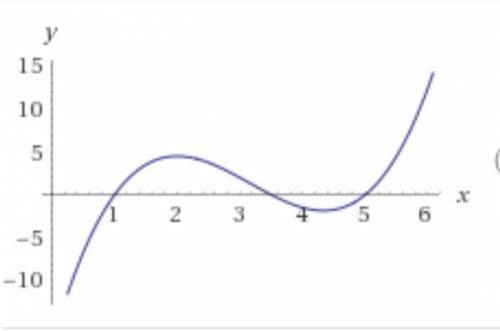
Будем считать, что надо найти корни заданного кубического выражения.
y=x^3-9,5x^2+26x-17,5 = 0.
Один корень явно виден - это х = 1.
Разделим многочлен на (х - 1):
x^3 - 9,5x^2 + 26x - 17,5 |x - 1
x^3 - x^2 x^2 - 8,5x + 17,5
-8,5x^2 + 26x
-8,5x^2 + 8,5x
-17,5x - 17,5
-17,5x - 17,5
0
Полученный квадратный трёхчлен разложим на множители, найдя его корни.
Решаем уравнение x^2 - 8,5*x + 17,5=0.
Ищем дискриминант:
D=(-8.5)^2-4*1*17.5=72.25-4*17.5=72.25-70=2.25;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(-(√2,25-8,5))/(2*1)=(1,5-(-8,5))/2=(1,5+8,5)/2=10/2=5;
x_2=(-√2,25-(-8,5))/(2*1)=(-1,5-(-8,5))/2=(-1,5+8,5)/2=7/2=3,5.
ответ: имеем три корня х = 1, х = 3,5 и х = 5.
Следующее число, которое в обоих направлениях читается одинаково - 16061.
Следовательно, за 2 часа автомобиль проехал 16061 - 15951 = 110 км, а его средняя скорость 110 / 2 = 55 км/ч.