Объяснение:
1) представьте систему в матричной форме
2) умножьте строку 1на (-2) и прибавить результат к строке 2
Умножьте строку 1на (-1) и прибавить результат к строке 3:
3) умножьте вторую строку на -1
4) умножить строку 3 на 2 и прибавить результат к строке 1.
Умножьте строку 3 на 5 и прибавьте результат к строке 2
5) разделить строку 2 на 14
6) умножить строку 2 на -7 и прибавить результат к строке 1.
Умножить строку 2 на -2 и прибавить результат к строке 3
7) умножить строку 3 на -1
8) преобразовать расширенную матрицу систему линейных уравнений
ответ: решение систем уравнений является упорядоченная тройка (х,у,z)
Решение на фотке

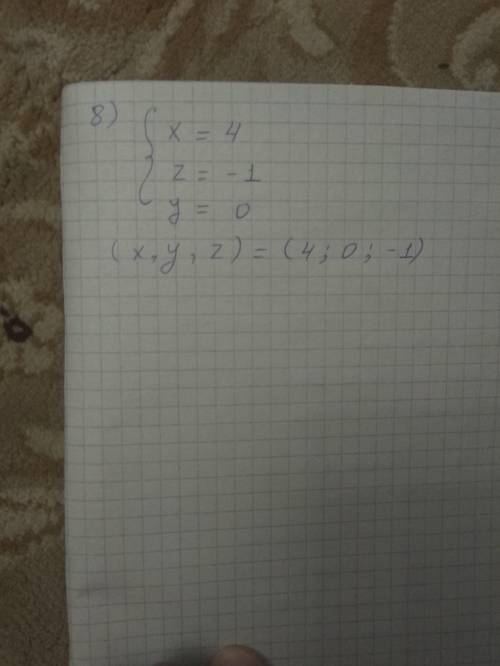
Т.к. b2=(b1 умножить на q), а b3=(b1 умножить на q^2), получаем
b1 + b2= b1 умножить на (1+q)=40
b2 + b3= b1 умножить на (q+q^2)=120 вынесем q за скобку, получим
b2 + b3= b1 умножить на q(1+q)=120, т.к. b1 умножить на (1+q)=40, то q =120/40=3 Найдём b1 из выражения b1 умножить на (1+q)=40
(1+3)b1=40, т.е. 4b1 =40 или b1=10
Чтобы найти сумму первых трёх членов прогрессии достаточно к сумме
(b2 + b3) добавить 10. Т.е 120+10=130
ответ: 130.