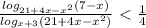
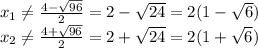
 ) U (
) U ( ; -2) U (-2;
; -2) U (-2;  ) U (
) U ( ; 7).
; 7).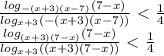
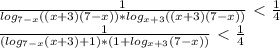
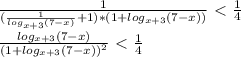
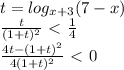
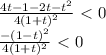
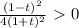
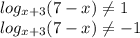
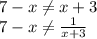
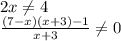
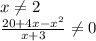
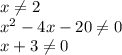
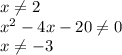
 ) U (
) U ( ; -2) U (-2; 2) U (2;
; -2) U (-2; 2) U (2;  ) U (
) U ( ; 7).
; 7).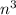 , по условию
, по условию 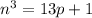 . Перенесём единицу в левую часть и разложим разность кубов на множители:
. Перенесём единицу в левую часть и разложим разность кубов на множители:
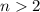 , тогда обе скобки-сомножителя - натуральные числа, большие 1. С другой стороны, произведение
, тогда обе скобки-сомножителя - натуральные числа, большие 1. С другой стороны, произведение 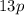 представляется в виде двух натуральных сомножителей, больших единицы, единственным (с точностью до перестановок
представляется в виде двух натуральных сомножителей, больших единицы, единственным (с точностью до перестановок 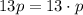 . Поэтому
. Поэтому  ,
,  равны либо
равны либо 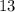 и
и 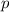 , либо
, либо 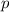 и
и 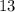 .
.
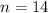 , тогда после подстановки во второе уравнение находим
, тогда после подстановки во второе уравнение находим 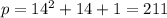 .
.  - действительно простое число, так что
- действительно простое число, так что 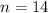 нас устраивает.
нас устраивает.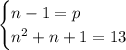
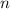 квадратное, а не линейное, как в первом случае. Упростив, получаем уравнение
квадратное, а не линейное, как в первом случае. Упростив, получаем уравнение 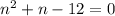 , у которого только один натуральный корень
, у которого только один натуральный корень 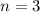 .
. - простое число, так что и тут нас всё устраивает.
- простое число, так что и тут нас всё устраивает. ,
, 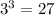
1) ищем производную
2) приравниваем к нулю, решаем получившееся уравнение
3) определяем, какие корни попадают в указанный промежуток
4) ищем значение функции на концах промежутка и в точке,
5) выбираем наибольший ответ
Начали.
1)Производная = 6/Cos²x - 6
2) 6/Cos²x - 6 =0
6/Cos²x = 6
Cos²x = 1
а) Cos x = 1 б) Cos x = -1
x = 2πk, где k∈Z x =πn,где n∈Z
3) Из этих ответов в указанный промежуток попадает только х =0
4) у = 6tg 0 - 6·0 +6 = 6
y = 6tg (-π/4) - 6·π/4 +6= -6 -6π/4 +6 = -3π/2
5) у =6