1. У равнобедренного треугольника углы при основании равны, поэтому угол при основании не может быть равен 108°, значит угол при вершине равнобедренного треугольника равен 108°, тогда углы при основании:
α = (180° - 108°)/2 = 36°
ответ: 36°.
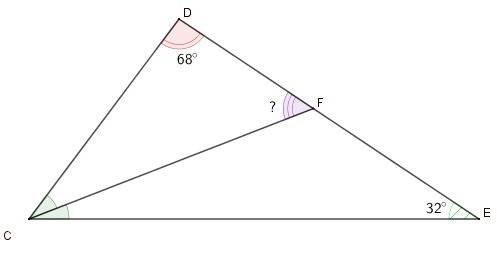
2) Полное условие. В треугольнике CDE проведена биссектриса CF, угол D=68*,угол E=32*. Найдите угол CFD.
Сумма внутренних углов треугольника равна 180°, поэтому
∠C = 180° - (∠D + ∠E) = 180° - (68°+32°) = 100°
Так как CF - биссектриса, то ∠DCF = ∠FCE = 0.5∠C = 50°
Рассмотрим треугольник CDF: ∠CFD = 180° - (∠CDF + ∠DCF)=62°
ответ: 62°
![lim_{x\to \infty }\frac{x+1}{x-2}=lim_{x\to \infty }\frac{\frac{x}{x}+\frac{1}{x}}{\frac{x}{x}-\frac{2}{x}}=lim\frac{1+\frac{1}{x}}{1-\frac{2}{x}}=[\frac{1+0}{1-0}]=\frac{1}{1}=1](/tpl/images/0237/6916/b2fde.png)
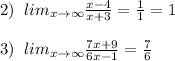
![lim_{x\to \infty }\frac{x+3}{5x^2+2x-5}=0,tak\; \; kak\\\\lim_{x\to \infty }\frac{\frac{x}{x^2}+\frac{3}{x^2}}{\frac{5x^2}{x^2}+\frac{2x}{x^2}-\frac{5}{x^2}}=lim\frac{\frac{1}{x}+\frac{3}{x^2}}{5+\frac{2}{x}-\frac{5}{x^2}}=[\frac{0+0}{5+0-0}]=\frac{0}{5}=0](/tpl/images/0237/6916/32e6e.png)
3c(c-5)=3c²-15c=(3*(-4)²)-(15*(-4)=(3*16)-60=48-60=-12
28 больше -12