Пусть за 
час 1-й кран будет наполнять весь бассейн
за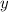 
час 2-й кран будет наполнять бассейн.
Если 1 - это объем всего бассейна, тогда
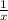- объем воды, который проходит через 1-й кран за 1 час.
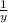- объем воды, который проходит через 2-й кран за 1 час.
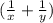- общая производительность двух кранов.
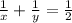- первое уравнение
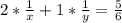- второе уравнение
Из первого уравнения получим: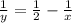 
и вставим во второе уравнение:
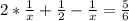
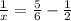
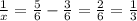
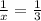
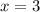
Подставим 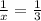в первое уравнение:
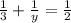
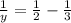
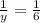
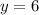
ответ: за 3 часа 1-й кран наполнит весь бассейн;
за 6 часов 2-й кран наполнит весь бассейн.
Для функции y(x)=x²-4x+3 найдите:
1 область определения функции;
2 множество значений функции;
3 наименьшее (наибольшее) значение функции;
4 уравнение оси симметрии параболы:
5 нули функции;
6 промежутки знакопостоянства функции;
7 промежутки монотонности функции
Объяснение:1. Область определения (-∞; +∞).
2. Область значений [-1; +∞).
3. Минимальное значение f(x) принимает в точке xmin = 2, f(2) = -1.
4. Ось симметрии x=2.
5. Нули функции x1=1, x2=3.
6. f(x)>0, при х∈(-∞;1)∪(3;+∞).
f(x)<0, при х∈(1;3).
7. f(x) убывает при х∈(-∞;2), f(x) возрастает при х∈(2;+∞).
Для функции y(x)=x²-4x+3 найдите:
1) область определения функции;
2)множество значений функции;
3)наименьшее (наибольшее) значение функции;
4)уравнение оси симметрии параболы:
5)нули функции;
6)промежутки знакопостоянства функции;
7)промежутки монотонности функции
f¹(x)=1/2(xsinx)⁻¹/²·(sinx+xcosx)=(sinx+xcosx)/2√(xsinx);
2. f(x)=x²/(x+5);⇒
f¹(x)=[2x(x+5)-x²]/(x+5)²=(x²+10x)/(x+5)²=x(x+10)/(x+5)²;
3.f(x)=x³/(5x-1);⇒
f¹(x)=[3x²·(5x-1)-5x³]/(5x-1)²=(15x³-3x²-5x³)/(5x-1)²=x²·(10x-3)/(5x-1)²;
4.f(x)=cosx+tgx;⇒
f¹(x)=-sinx+1/cos²x=cos⁻²x-sinx;
5.f(x)=2ctgx-sinx;⇒
f¹(x)=2/(-sin²x)-cosx=-2/sin²x - cosx;
6.f(x)=3x⁴/sinx;⇒
f¹(x)=(12x³sinx-3x⁴cosx)/sin²x=x³·(12sinx-3xcosx)/sin²x;
7.f(x)=cosx/2x³;⇒
f¹(x)=(-2x³sinx-6x²cosx)/4x⁶=-x²·(xsinx+3cosx)/2x⁶=-(xsinx+3cosx)/2x⁴;
8,f(x)=(x-5)(x²+7)=x³-5x²+7x-35;⇒
f¹(x)=3x²-10x+7;
9.f(x)=(2x³-3)(1/x+1);⇒
f¹(x)=[6x²(1/x+1)-(2x³-3)(-1)x⁻²]/(1/x+1)²=(6x+6x²+2x-3x⁻²)/(1/x+1)²=(8x+6x²-3x⁻²)/(1/x+1)²;
10.f(x)=(7x-2)⁵;⇒
f¹(x)=5·(7x-2)⁴·7=35(7x-2)⁴;
11.f(x)=(4-9x)⁶;⇒f¹(x)=6·(4-9x)⁵·(-9)=-54(4-9x)⁵;
12.f(x)=10cos3x;⇒f¹(x)=10·3·(-sin3x)=-30sin3x;
13.f(x)=sin(2x+π/6);⇒f¹(x)=2cos(2x+π/6);
14.f(x)=√(25x-7)=(25x-7)¹/²;⇒f¹(x)=25·1/2·(25x-7)⁻¹/²=25/2√(25x-7);
15.f(x)=√(17-12x);⇒f¹(x)=-12/2√(17-12x);
16.f(x)=tg2x;⇒f¹(x)=2·1/cos²2x=2/cos²2x;
17.f(x)=ctg(x+7);⇒f¹(x)=-1/sin²(x+7);
18.f(x)=x√x=x^(3/2);⇒f¹(x)=3/2·x^(1/2)=3/2·√x;
19.f(x)=cos²x;⇒f¹(x)=2·cosx·(-sinx)=-2cosxsinx=-sin2x;
20.f(x)=sin³x;⇒f¹(x)=3·sin²x·cosx;