а) sin x - 0,5 = 0
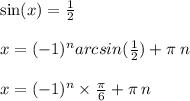
*где n - целое число
Рассмотрим варианты:
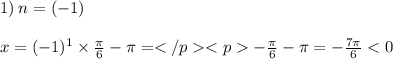
При n=(-1) - х<0 и не принадлежит отрезку [0;2π].
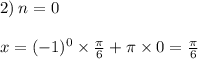
При n=0 - x = π/6 - принадлежит отрезку [0;2π].
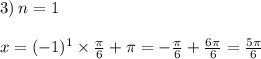
При n=1 - x = (5π/6) - принадлежит отрезку [0;2π].
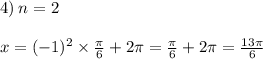
При n=2 - x = (13π/6) - не принадлежит отрезку [0;2π].
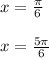
б) tg x - 1 = 0
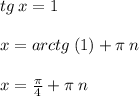
*где n - целое число
Рассмотрим варианты:
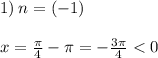
При n=(-1) - х<0 и не принадлежит отрезку [0;2π].
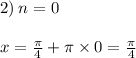
При n=0 - x = π/4 - принадлежит отрезку [0;2π].
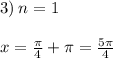
При n=1 - x = (5π/4) - принадлежит отрезку [0;2π].
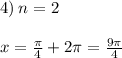
При n=2 - x = (9π/4) - не принадлежит отрезку [0;2π].
![Найдите корни уравнения, принадлежащие отрезку [0;2пи]: а) sin x - 0,5 = 0; б) tg x - 1 = 0.](/tpl/images/4836/4198/1fe1b.jpg)
Объяснение:
| 7 - x | - | x - 10 | ;
вирази під модулем дорівнюють 0 при х = 7 і х = 10 , тому
умову x < 10 розбиваємо на дві (- ∞ ; 7] i ( 7 ; 10 ) :
1 ) при хЄ (- ∞ ; 7] , | 7 - x | - | x - 10 | = 7 - х + х - 10 = - 3 ;
2 ) при хЄ ( 7 ; 10 ) , | 7 - x | - | x - 10 | = - ( 7 - х ) + х - 10 = 2х - 17 .
Отже ,
| 7 - x | - | x - 10 | = { - 3 , якщо х ≤ 7 ,
{ 2x - 17, якщо 7 < x < 10 .
х - 2 - сторона 2-го
S1 = x^2 - площадь 1-го квадрата
S2 = (x-2)^2 - площадь 2-го
S1 = S2 + 12
x^2 = (x-2)^2 + 12
x^2 = x^2 - 4x + 4 + 12
4x = 16
x = 4 см - сторона 1-го квадрата
х-2 = 4-2 = 2 см - сторона 2-го квадрата
Р1 - 4 * х = 4 * 4 = 16 см - периметр 1-го квадрата
Р2 = 4 * (х-2) = 4 * (4-2) =8 см - периметр