1/6
Объяснение:
Вероятность Р=m/n, где n- общее число элементарных исходов, m - число благоприятных элементарных исходов.
При бросании игрального кубика равновероятно наступление следующих шести исходов: - выпадение "1", выпадение "2", выпадение "3", выпадение "4", выпадение "5", выпадение "6". Значит, n=6
Из них только "5" делится без остатка на 5. Значит, m=1
Следовательно, вероятность того, что количество выпавших очков на верхней грани кубика будет числом, которое делится на 5 равна
Р = 1/6.
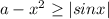
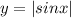расположен выше оси ОХ. 
.
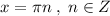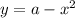- это параболы , ветви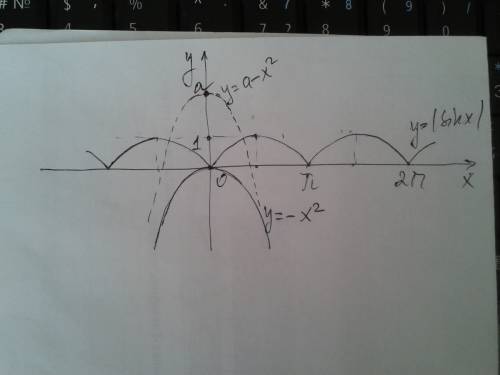
2x^2=32 | :2
x^2=16
x1,2=+-8
2) 4x2 + 4x + 1 = 0
D = b2 - 4ac = 42 - 4∙4∙1 = 0
D = 0 ⇒ уравнение имеет один корень
x = -b/2a = -4/(2∙4) = -0.5
ответ: x=-0,5
3) -x^2+ 7x + 8 = 0
D = b2 - 4ac = 72 - 4∙(-1)∙8 = 81
D > 0 ⇒ уравнение имеет 2 корня
x = -b ± √D / 2a
x1 = (-7 - √81) / (2∙-1) = 8
x2 = (-7 + √81) / (2∙-1) = -1
ответ: x = 8; -1
4) x2 - 2x - 15 = 0
D = b2 - 4ac = (-2)2 - 4∙1∙(-15) = 64
D > 0 ⇒ уравнение имеет 2 корня
x = -b ± √D / 2a
x1 = (2 - √64) / (2∙1) = -3
x2 = (2 + √64) / (2∙1) = 5
ответ: x = -3; 5
5) 5x2 - 8x - 4 = 0
D = b2 - 4ac = (-8)2 - 4∙5∙(-4) = 144
D > 0 ⇒ уравнение имеет 2 корня
x = -b ± √D / 2a
x1 = (8 - √144) / (2∙5) = -0.4
x2 = (8 + √144) / (2∙5) = 2
ответ: x = -0.4; 2
6) 6x2 - 7x + 1 = 0
D = b2 - 4ac = (-7)2 - 4∙6∙1 = 25
D > 0 ⇒ уравнение имеет 2 корня
x = -b ± √D / 2a
x1 = (7 - √25) / (2∙6) = 0.166666666667
x2 = (7 + √25) / (2∙6) = 1
ответ: x = 0.2; 1