

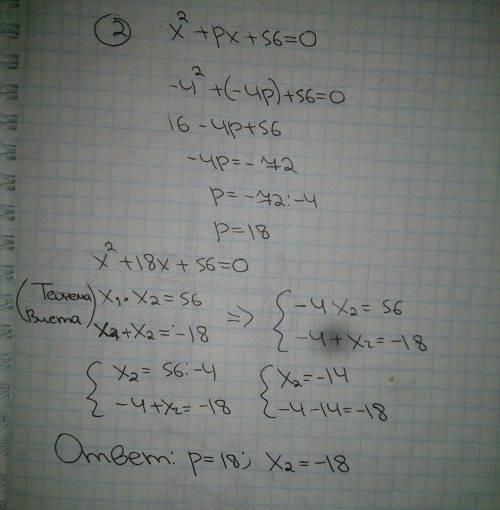
Объяснение:
1а) x² + x - 20 ≠0
найдем x² + x - 20 = 0
D = 1+80 = 81
x ₁ ₂ = (-1 ±9) / 2
x₁ = -5
x₂ = 4
ОВФ (-∞; -5)∩ (-5;4)∩(4; +∞)
1б) получитсясистема:
{x+9 ≥0 {x≥-9
{4-x ≥0 {x ≤4
ОВФ [-9;4]
2a) f(-x) = -4x⁷ +2x³ = -f(x) нечетная
2б) f(-x) = (-x)² -3(-x)⁴= x² -3x⁴ = f(x) четная
2в) f(-x) = -x³ + (-x)⁶ = -x³ + x⁶ ≠ f(x) ≠ f(x) ни четная, ни нечетная
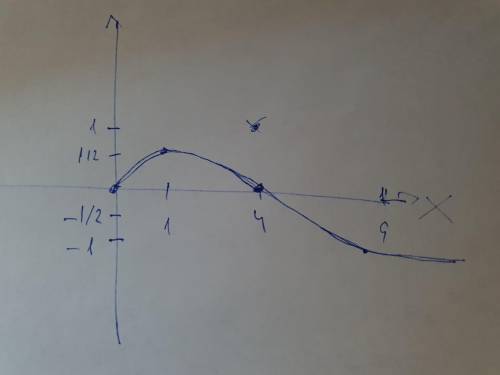
3) область определения X≥0
а) пересечение с x т. е. y =0 при х = 0 и x = 4 точки (0;0), (4;0)
б) возрастание [0;1]
убывание (1;+∞)
в) ОЗФ, [0.5; +∞)
ответ: ОДЗ: х не равно -3; х не равно о.
переносим 3 в левую часть.
дополнительный множитель к первой дроби х, ко второй х+з, к третей х(х+3)
раскрывает скобки и у нас получается в числителе 5х+4х+12-3х^2-9х в знаменателе х(х+3)
уничтожаем подобные члены и у нас остается +12-3х^2/х(х+3)>=0
умножаем на -1 и у нас получается (когда мы умножаем на -1 знак тоже меняется)
3х^2+12/х(х+3)<=0
теперь выносим 3 и у нас получается 3(х^2-4)/х(х+3)<=0
теперь раскладываем на множители в скобке
3(х-2)(х+2)/х(х+3)<=0
воспользуемся методом интервалов,а для этого найдем нули функции
f(x)=f(0)=f(-2)=f(2)=f(-3)
теперь нули вынесем на координатную прямую
___-3-202>
ответ х=(-3;-2]u(0;2]