Решить на координатной прямой отмечены числа а и b. какое из следующих утверждений неверно? в ответе укажите номер правильного варианта. 1) а+b< 0 2) -4< a-1< 0 3) a2 8 < 0 4) -b< 0 известно, что a< b< 0 выберите наименьшее из чисел. 1)a-1 2)b-2 3)ab 4)-b
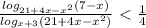
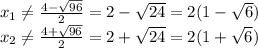
 ) U (
) U ( ; -2) U (-2;
; -2) U (-2;  ) U (
) U ( ; 7).
; 7).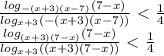
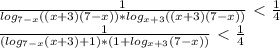
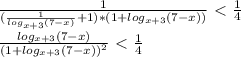
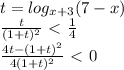
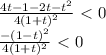
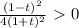
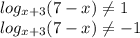
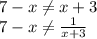
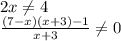
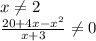
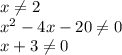
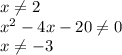
 ) U (
) U ( ; -2) U (-2; 2) U (2;
; -2) U (-2; 2) U (2;  ) U (
) U ( ; 7).
; 7).
Дано: -3<a<-2
-1<b<0
1) а+b< 0 - верно: (-)+(-)=(-)
2) -4< a-1< 0 - верно: -3<a => -4<a-1; a<-2 => a-1<-3, значит a<0.
3) a²b < 0 - верно: (-)²=(+), (+)*(-)=(-)
4) -b< 0 - неверно: -(-)=(-)*(-)=(+) => -b>0
Выбрать наименьшее из чисел:
1) a-1 - a<-2 => a-1<-3
2) b-2 - b<0 => b-2<-2
3) ab - (-)*(-)=(+) => произведение ab - это положительное число
4) -b - -(-)=(-)*(-)=(+) =Ю=> -b - положительное число.
Наименьшее из чисел - это а-1, которое меньше -3.