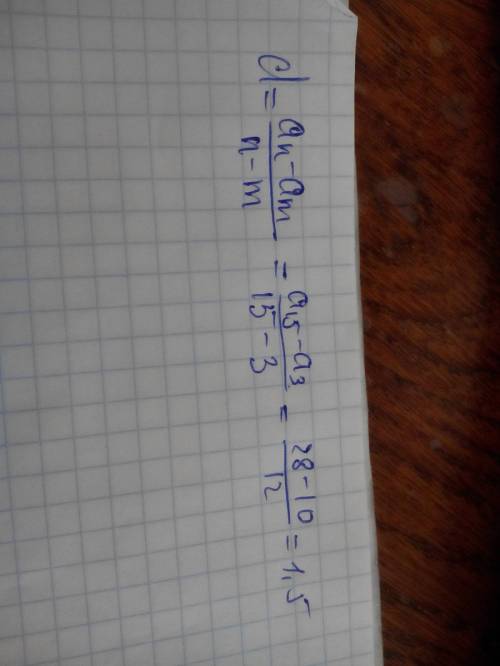
По условию задачи имеем две неизвестных переменных, переменная t=времени,пер-
еменная х=скорости течения реки.Составим систему линейных уравнений с двумя
переменными.
10t+xt=70 1 уравнение системы ,показывает сколько лодка по течению.
10t-xt=30 2 уравнение системы показывает сколько лодка против.
Решим систему уравнений сложения.xt и -xt противоположные числа при
сложении дают 0. Сложим почленно каждый член 1 ур с чл 2 ур получим
20t=100 выразим t, t=100:20=>t=5; Решим 2 уравнение с 1 переменной
10*5-5x=30,=>50-5x=30,=>-5х=30-50,=>-х=-20:5,=>-х=-4 значит х=4.
ответ:скорость течения реки равна 4 км/ч,а время 5 часам.
Подробно:
Пусть первый рабочий делает х деталей в час.
Тогда второй рабочий делает х-3 детали в час.
Первый рабочий сделает 391 детали за
391:х часов
второй рабочий сделает 460 деталей за
460:(х-3)
По условию задачи время первого рабочего при изготовлении 391 детали меньше времени второго рабочего при изготовлении 460 деталей на 6 часов.
Запишем и решим уравнение:
460:(х-3) - 391:х =6
Умножим обе части уравнения на х(х-3)
460х - 391(х-3) =6 х(х-3)
460х - 391х+1173 =6 х²-18х
6 х² -69х-18х - 1173=0
6 х² -87х - 1173=0
для облегчения вычислений разделим на 3 обе части уравнения
2 х² - 29х-391=0
Дискриминант равен:
D=b2-4ac=-292-4·2·-391=3969
У уравнения 2 корня.
х=23
Второй корень отрицательный, он не подходит.
Первый рабочий делает в час 23 детали.
Проверка:
460:(23-3) -391:23=6
Коротко:
Пусть первый рабочий делает х деталей в час.
Тогда второй рабочий делает х-3 детали в час.
Составим и решим уравнение
460:(х-3) - 391:х =6
6 х² -87х - 1173=0
Дискриминант равен:
D=b2-4ac=-292-4·2·-391=3969
х=23
ответ:23 детали в час