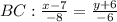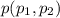,
.
в прямоугольной системе координат, то вектор 
является вектором нормали данной прямой.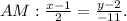
Уравнение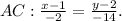 
Или в общем виде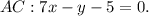 
Нормальный вектор стороны АС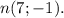 
, а для высоты ВН он будет направляющим:
Уравнение высоты 
Или в общем виде: -х + 7 = 7у + 42,
х + 7у + 35 = 0.
x^4-4x^2=0
х1=0; х2=2; х3=-2;
Для нахождения экстреммумов функции нужно взять производную и прировнять ее 0
f(x)=x^4-4x^2 => f'(x)=4*x^3-8x=0
Корни: х1=0; х2=2^0.5; х3=-2^0.5; (корень квадратный из 2)
теперь нужно узнать, что это за точки минимумы или максимумы, возмем значение слева и справа от точки и подставим в уранение если знак меняется с + на - значит максимум если наоборот минимум
-2^0.5 0 2^0.5
---*---о*о*---о*--
-2 -1 1 2
x=0 => y= 0
x=-2^0.5 => y= -4
x=2^0.5 => y= -4
x=-2 => y= 0
x=-1 => y=-3
x=1 => y=-3
x=2 => y= 0
Значение функции меняется от -2 до -2^0.5 функция убывает от 0 до -4 , а от -2^0.5 до -1 ворастает от -4 до -3 следовательно f(-2^0.5) минимум.
Значение функции меняется от -1 до 0 функция возрастает от -3 до 0 , а 0 до 1 убывает от 0 до -3 следовательно f(0) максимум.
Значение функции меняется от 1 до 2^0.5 функция убывает от -3 до -4 , а от 2^0.5 до 2 ворастает от -4 до 0 следовательно f(2^0.5) минимум.
Исследование завершено
Точки пересечения с осью Х
х1=0; х2=2; х3=-2;
Минимум
(-2^0.5;-4) и (2^0.5;-4)
Максимум
(0;0)