
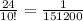

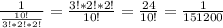
1 2 2
Объяснение:
Разберемся что такое натуральные числа, это те числа которые образованны естественным образом при счете то есть 1, 2, 3, 4, 5, 6, 7, 8,
все натуральные числа расположены в порядке возрастания.
То есть смотри берем одну двойку возводим ее в квадрат получается 2*2=4 допустим берем три 3*3=9 значит тройка сразу отпадает, берем еще одну двойку 2*2=4 уже получается 4+4=8 и берем единицу, а все мы знаем что при возведении единицы в квадрат будет единица, и того 8+1=9. Таким образом мы получили 3 натуральных числа сумма которых ровняется девяти
Производная функции в точке
ответ: 67.
Значение производной функции в точке
ответ: -1.
3) По формуле производной произведения: , имеем
, имеем
Вычислим значение производной функции в точке
ответ: -1.
4) Аналогично применяем формулу из примера 3)
Найдем значение производной функции в точке
ответ: 1.